Аннотация

Предлагается стохастический параллельный алгоритм оценивания числа стимулов при одномоментном восприятии. Определяются вероятностные характеристики достоверности оценки числа поступивших стимулов и оценивается быстродействие алгоритма. Показано, что рассмотренный алгоритм обладает характеристиками, сходными с основными характеристиками сенсорных систем биологических объектов при оценке числа стимулов.

Зрительная система животных позволяет с высокой достоверностью оценивать небольшое число элементов изображений (например, точек или пятен), предъявляемых на короткий интервал времени [1].

При этом по мере увеличения числа стимулов (выше шести-семи) достоверность оценивания снижается. Аналогичные свойства обнаружены у кожного анализатора, у слухового анализатора и у других. Можно предположить [2], что в основе общности свойств указанных анализаторов лежат свойства универсального алгоритма.

Анализ процесса одномоментного восприятия позволяет выдвинуть следующие предположения о свойствах этого алгоритма:

Во-первых, алгоритм не связан со сканированием выходов всех волокон афферентного нерва. При времени опроса одного волокна порядка 10^-3 с и числе нервных волокон зрительного нерва порядка 1.10⁸ сканирование всего нерва для оценки числа предъявленных стимулов потребовало бы не менее 10³с. Зрительным анализатором оценивание числа предъявленных стимулов производится за десятые доли секунды; из чего следует, что основная обработка информации о числе стимулов производится одновременно (параллельно).

Во-вторых, рассматриваемый алгоритм является стохастическим, так как при оценивании числа стимулов (например, чёрных точек на светлом фоне) анализатор дает недетерминированный ответ, причем с увеличением числа стимулов вероятность правильного оценивания снижается.

Моделирование алгоритмов реализованных в мозге необходимо для создания технических интеллектуальных систем. Особый интерес представляют алгоритмы, обеспечивающие параллельную обработку информации.

Рассмотрим устройство, реализующее алгоритм, который может послужить моделью алгоритма, существующего в биологических анализаторах. В технике применяется преобразование совокупности одновременно (параллельно) поступивших сигналов в последовательность сигналов. На рис. 1 изображена блок-схема такого устройства.

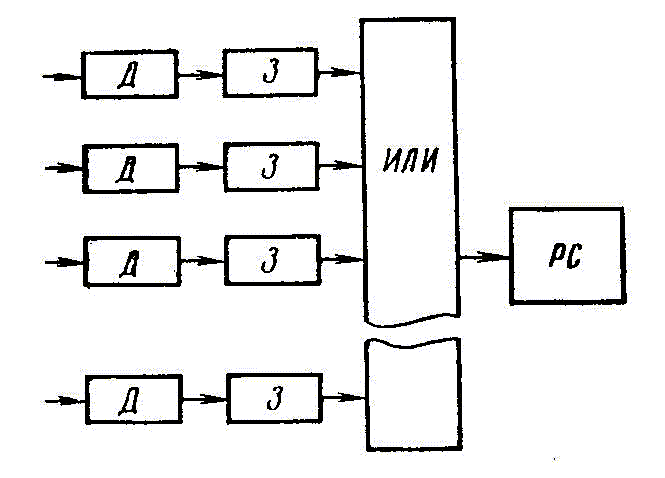Рис. 1

Анализируемый сложный сигнал, содержащий несколько стимулов, поступает на поле датчиков. Каждый датчик "Д" в данном случае моделирует функции рецептивного поля [2, 3, 4]. Общим является требование, чтобы датчик реагировал на различные значения стимулирующего воздействия в двоичном коде. Для этого датчик должен содержать специализированный входной преобразователь и пороговый элемент. Специализированный входной преобразователь преобразует стимулирующее воздействие в аналоговую величину. При моделировании зрительного анализатора роль такого преобразователя выполняют фотодатчики (фоторезисторы, фотодиоды).

В дальнейшем предполагается, что каждый стимул активизирует только один датчик. Датчики "Д", образующие поле датчиков, соединены с элементами задержки 3. Выходы всех элементов задержки присоединены к входам схемы "ИЛИ". К выходу схемы "ИЛИ" присоединен регистрирующий счетчик "РС" числа сигналов.

Прототипом поля фотодатчиков является сетчатка глаза, прототипами элементов задержки можно считать нервные волокна, а функции схемы "ИЛИ" и регистрирующего счетчика предположительно выполняются на более высоких уровнях нервной системы.

Рассмотрим рабочий цикл данного устройства. В течение малого времени (интервала экспозиции) на поле датчиков поступает ограниченноe число стимулов. Так как стимулирующие воздействия случайно распределены по полю датчиков и величины элементов задержки, присоединенных к датчикам, выбраны случайно, произойдет разделение сигналов во времени.

На выходе логической схемы "ИЛИ" появится последовательность импульсов, число которых фиксируется при помощи регистрирующего счетчика "РС" небольшой емкости.

Существует отличная от нуля вероятность того, что все сигналы, сформированные активизированными датчиками, будут задержаны на различные интервалы времени и в регистрирующем счетчике будет зафиксировано число поступивших стимулов. Эта вероятность зависит от разрешающей способности счетчика, а также от числа поступивших стимулов. Разрешающей способностью счетчика является минимальный интервал времени между двумя сигналами, которые счетчик еще может воспринять раздельно.

Предположим, что время задержки сигналов является непрерывной случайной величиной, равномерно распределенной на интервале  . Разрешающую способность счётчика  зададим как долю интервала  :

где  . Если хотя бы два сигнала поступят на схему "ИЛИ", разделенные во времени меньше чем на , то "РС" зафиксирует, их как один сигнал и произойдет ошибочное оценивание числа поступивших стимулов. При двух стимулах, поступивших на поле датчиков, возникает задача, которая в теории вероятностей носит название «задачи о встрече» [5]. Для m стимулов можно сформулировать многомерную «задачу о встрече». В рассматриваемом устройстве «встреча» двух или более сигналов приводит к ошибке в оценивании числа стимулов, поступивших на поле датчиков. На рис. 2 приведены зависимости вероятности правильного оцениванияР_m от числа поступивших стимулов при двух значениях параметра . Эти зависимости получены в результате моделирования многомерной «задачи о встрече» на ЭВМ.

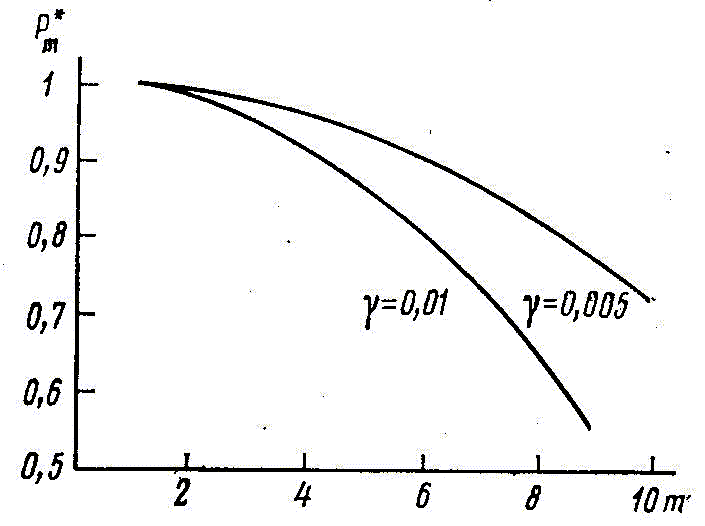Рис. 2

Анализ полученных зависимостей подтверждает вывод о том, что рассмотренный алгоритм обладает характеристиками, сходными с основными характеристиками сенсорных систем биологических объектов.

Стохастические алгоритмы, подобные рассмотренному, редко используются в технике. Между тем, проведённый выше анализ показывает, что в данном случае удаётся обеспечить высокое быстродействие при контролируемой величине погрешности. В зависимостях, приведённых на рис.2, проявляется своеобразное „соотношение неопределённости“ --при уменьшении времени оценки параметра увеличивается погрешность оценки.

ЛИТЕРАТУРА

1. Миллер Дж. А. Магическое число семь, плюс или минус два. О некоторых пределах нашей способности перерабатывать информацию.— В кн.: Инженерная психология. М.: Прогресс, 1964, с. 192-225.
2. Щербанский Л. М. О структуре алгоритма оценивания числа стимулов при одномоментном восприятии. Автоматика и Телемеханика, 1982, № 4, с. 50-53.
3. Агабабян К. Г. Об алгебре нейронных матриц.—Докл. АН СССР (сер. математика, физика), 1971, т. 199, № 5, с. 991-993.
4.Физиология сенсорных систем (под общей ред. чл.корр. РАН, проф. Я.А.Альтмана) СПб.: "Паритет", 2003.
5. Гнеденко Б.В. Курс теории вероятностей: Учебник для университетов. 7-е издание. – М.: Эдиториал УРСС, 2001.

Статья поступила в редакцию 10 января 2007 года