Аннотация 

В статье предлагается новая точка зрения на марсилианскую табличку, найденную в греческом некрополе VII в. до н.э. в Италии. Выдвигается предположение, что эта табличка является счётной доской-абецедарием для арифметических расчётов с числами, записанными в алфавитной нумерационной системе. Приводится пример сложения на счётной доске подобного типа в более поздней греческой (ионической) алфавитной системе.

В начале XX в. в селении Марсилиана, расположенном в 20 км от берега Тирренского залива, в нижнем течении р. Албенья (Marsigliana d’Albegna) в Северной Италии производились раскопки большого некрополя у греческого поселения в древней греческой колонии на территории Этрурии. Некрополь датируется примерно 700 – 650 г до н.э.¹ Поселение представляло собой колонию греков, прибывших с о.Эвбея, расположенного у материковой Греции. Сначала они жили на «Обезьяньем» (Pithecusae) острове ² (греки попали на необитаемый остров в нынешнем Тирренском заливе, кишащий обезьянами на деревьях), но позже, после сильного землетрясения (Везувий-то совсем рядом) перебрались на материк, в место, которое сейчас занимает селение Марсилиана. В некрополе вблизи этого поселения и была обнаружена дощечка из слоновой кости вместе со «стилем» - костяной палочкой для письма по воску, остатки которого обнаружены на внутреннем прямоугольном поле таблички (рис. 1). Эта «марсилианская табличка» хранится в Археологическом музее во Флоренции и неоднократно описана в литературе³ . Особенность этой таблички в том, что абецедарий⁴ (представленный западно-греческим алфавитом VII в. до н.э.) на верхнем бортике записан справа налево, т.е. в направлении, противоположном направлению греческого письма. Этот факт всегда смущал исследователей. В своей классической работе Джеффери, описывая алфавит этого абецедария ⁵, отмечала, что он, как и некоторых другие абецедарии, найденные в соседних местах, является эвбейским, но это единственный пример (выделено мною – М.Ц.) алфавитной последовательности, которая записана справа налево. До сего времени специалисты-археологи не могут определённо указать назначение этой таблички. 
По моему мнению, эта табличка является греческой счётной доской-абецедарием для вычислений с числами, записанными в греческом числовом алфавите того времени. Я показал⁶ , что на счётной доске-абецедарии должен быть именно такой обратный порядок, чтобы получать числа, состоящие из компонентов, записанных в правильном порядке, т.е. старшие разряды слева, а младшие – справа. 
Систему алфавитной записи чисел греки скопировали у египтян (у которых она зафиксирована в иератическом и демотическом скриптах), смысл этой системы состоял в том, что для каждого вида единиц (от 1 до 9) существовала эннеяда (девятка, по-гречески) знаков, эннеяда других знаков – для десятков (от 10 до 90), по эннеяде для сотен (от 100 до 900) и тысяч (от 1000 до 9000). У египтян для записи чисел применялись специальные знаки, не имеющие применения для записи звуков. Греки, в отличие от египтян, использовали для этой цели свой алфавит, т.е. буквы, применявшиеся и для записи звуков. В ранне-греческие времена, к которым относится VII в. до н.э., многие греческие города-государства имели свои собственные алфавиты. Есть много оснований предпологать, что греки также использовали свой местный алфавит для записи чисел. В таблице 1 приведены возможные значения чисел, записываемых буквами эвбейского алфавита

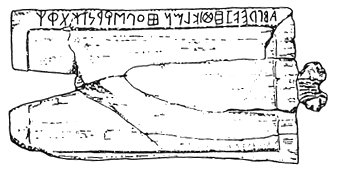Рис.1. Марсилианская табличка (ок. 700 г до н.э.)⁷ .
Её размеры 2 дюйма x 3¹/₂ дюйма (51 мм x 89 мм).
Внутреннее прямоугольное поле заполнялось слоем воска, следы которого сохранились.

Таблица 1. Возможные числовые значения букв на
марсилианской табличке.

Я не настаиваю на 100%-ной истинности записанных в таблице 1 возможных числовых значений букв на марсилианской табличке, повидимому, дальнейшие исследования текстов, записанных эвбейским алфавитом и включающих записи чисел, позволят уточнить какие-то детали. 
Позже, в 403 г. до н.э. в Афинах была произведена унификация греческого алфавита. Для записи чисел греки использовали свой алфавит (24 знака) и три устаревших буквы (эписемы) – всего 27 знаков, т.е. три эннеяды, для единиц, десятков и сотен. В таблице 2 приведены знаки унифицированного греческого числового алфавита (т.н. ионическая система нумерации). 
Не буду распространяться о мелких деталях записи чисел (например, чтобы отличить число от словесного текста, над всеми буквами числа проводили горизонтальную черту, были приёмы записи чисел, равных единицам тысяч и пр.), об этом подробно расписано в литературе⁸. Кстати, греки в те времена уже писали слева направо, и числа записывали по манере, принятой ещё в древнем Вавилоне. Тогда знаки сложения и вычитания (наши + и -) ещё не существовали, слагаемые записывали впритык друг к другу. Если левое слагаемое было по своей величине больше правого, то такие числа суммировались. Если же наоборот, левое число было меньше правого, то такое левое вычиталось из правого и результат воспринимался как разность. Мы это хорошо знаем по более поздним римским числам: IX = 9, XL = 40, XC = 90. Поэтому, чтобы записать число как сумму компонентов, надо было слева поместить самый большой компонент, а правее – меньшие. И поскольку любой десяток больше любой единицы, а любая сотня больше любого десятка, сложилось правило: писать сначала (слева) сотни, потом десятки и потом – единицы. 
Записать число – это ещё полдела. Как складывать и вычитать числа, записанные подобным образом? Для этой цели существовала счётная доска (абак-абецедарий). Схема счёта на абаке-абецедарии применительно к ионической алфавитно-числовой системе показана на рис 2. Компоненты чисел отмечались камнями (псефотами, по-гречески). На этом рисунке показан пример сложения двух чисел. Основной принцип сложения: камни единиц надо складывать с камнями единиц, камни десятков – с десятками, камни сотен – с сотнями. При добавлении одного камня единиц к существующим камням единиц, камень результата передвигается влево на одну позицию. Если количество камней единиц превысило девять (θ), то все камни единиц снимаются с доски и заменяются одним камнем десятка, добавляемым к камням десятков. Тот же принцип применяется и по отношению к десяткам и сотням. И наоборот, при вычитании, если надо вычесть единицу, а у вычитаемого числа нет камней в разряде единиц, то в разряде десятков занимается один десяток (т.е. камень десятков передвигается вправо на одну позицию), из этого занятого десятка вычитается единица, и в результат выкладываются остальные девять единиц (на позицию θ).

Таблица 2. Греческий числовой алфавит.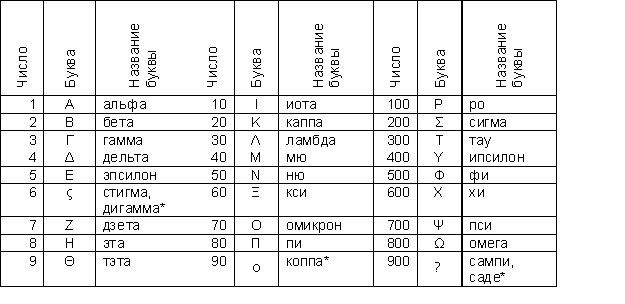Примечание: * - устаревшие буквы (эписемы), используемые только для обозначения числовых значений

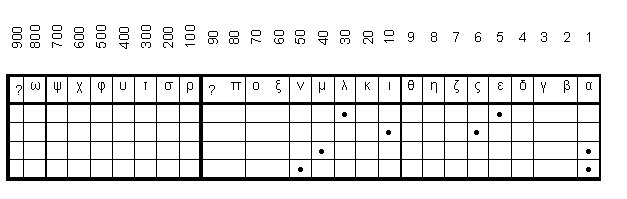Рис.2. Сложение двух чисел на греческой счётной доске-абецедарии: λε + ις (35 + 16).
В первой строке – первое число (λε), во второй строке – второе число (ις).
В третьей строке –к первому числу добавлены единицы (ς) из второго числа 
(промежуточный результат - μα). В четвёртой строке – к промежуточному
результату добавлены десятки второго числа (ι). Окончательный результат - να (51).

Можно уверенно предполагать, что вышеописанная система счёта с помощью абака-абецедария не была придумана греками, она была скопирована с египетского аналога. Об этом говорит марсилианская табличка. Изготовление её из слоновой кости, использование воска для записи компонентов чисел (вместо камня-псефота вычислитель делал стилем ямку в воске в соответствующем месте, при перемещении псефота ямка заравнивалась лопаточкой на противоположном конце стиля) и другие признаки говорят, что это было серийное изделие, а не опытный образец. 
Для умножения египтяне применяли способ, использующий сложение удваемых компонентов (подробности описаны в литературе⁹). 
Таким образом, вполне вероятно, что уже в VII в. до н.э. греки имели свой «наладонный» компьютер. Именно так можно рассматривать «марсилианскую» табличку.

Автор выражает благодарность Наталии Гольдбаум за помощь в подготовке этой статьи.

¹ Minto, A., Marsigliana d’Albegna. 1921.; Buonamici, G., Epigrafia Etrusca (Florence 1932), 128 ff.
² Ныне о.Искья.
³Von Vacano, O.-W. The Etruscans in the Ancient World. (Transl. Ogilvie, S.A.) London: Edward Arnold. 1960, p.34; Немировский А.И., Этруски (от мифа к истории),М., Наука, 1983, с.71.
⁴ Абецедарием называется последовательность букв, записанных в алфавитном порядке.
⁵ Jeffery, L.H., The Local Scripts of Archaic Greece. Oxford: Clarendon Press, 1961, p. 236 ff.
⁶ Цайгер М.А., Арифметика у древних славян и в допетровской России, ВИЕТ, 2007, № 2, с. 20-40. О конструкции абака-абецедария и арифметических действиях на нём см. с. 28 и далее.
⁷ Рисунок со стр. 1, The University of Oklahoma, Classes online, Etruscan Art, Language, (http://www.ou.edu/class/ahi4163/slides3/alphabet.gif).
⁸ См., например, Heath T.L. , 1921, History of Greek Mathematics, Oxford, Clarendon Press, vol.I.
⁹ Gillings R.J. , 1972, Mathematics in the Time of Pharaohs. Cambridge, Mass.