- Abstract
The present paper considers from a new standpoint the purpose of Marsiliana tablet which was found in Italy in an early Greek necropolis of VII century BC. It is suggested that this tablet is a counter board – abecedarium for performing arithmetic operations with integer numbers written in alphabetic numerical system. An example of performing addition by means of a counter board of this type using a later Ionic alphabetic system is presented.
Sommario
Lo scritto presente considera da un nuovo punto di vista lo scopo della tabella di Marsigiana che e stata trovata in Italia in un'antica necropoli greca del secolo VII aC. Si suggerisce che questa e una tabella contatore - abecedarium per l'esecuzione dei operazioni aritmetiche con numeri interi scritti in conformita alla sistema alfabetica numerica. Un esempio dell'addizione dei numeri per mezzo della tabella contatore di questo tipo utilizzando la sistema alfabetica ionica piu tarda e presentato.
In the beginning of the XX century, in the settlement Marsiliana located in 20 km from the coast of the Tyrrhenian Sea, in the lower reach of Albegna river (Marsigliana d’Albegna) in Northern Italy, excavations of a big necropolis at an ancient Greek settlement in the territory of Etruria were carried out. The necropolis is dated as approximately 700 – 650 BC [Minto, 1921; Buonamici, 1932]. The settlement represented a colony of Greeks who had arrived from Euboea island located near the continental Greece. First they lived on the Monkey's (Pithecusae) island1 (Greeks had got on an uninhabited island in the Tyrrhenian Sea, teeming with monkeys on trees), but later, after a strong earthquake (the volcano Vesuvius being nearby) got over to the continent, to the place where Marsiliana settlement is now located. In the necropolis near this settlement a plate from ivory has been found together with a stylus – a bone stick for writing on wax, whose traces were revealed on the internal rectangular area of the tablet (Fig. 1). This Marsiliana tablet is now kept in the Archaeological Museum in Florence and has been described in the literature more than once [Von Vacano, 1960, 34; Nemirovsky, 1983, 71 ]. A peculiar feature of this tablet is that abecedarium2 (represented by the West-Greek alphabet of the VII century BC) on its upper edge is written from right to left, i.e. in the direction opposite to the direction of the Greek script. This fact has always confused researchers. In the classical work of Jeffery describing the alphabet of this abecedarium [Jeffery, 1961, 236 ff.], it was noted that it, as well as some other abecedaria found in neighboring places, is Euboean, but this is the only example of an alphabetical sequence written from right to left ([Jeffery, 1961, 237], italisized by me – M.Ts.). To this time, experts-archeologists cannot specify the function of this tablet definitely.
In my opinion, this tablet is a Greek counter board-abecedarium for calculations with numbers written using Greek numerical alphabet of that time. As I have shown [Tsayger, 2007, 28 ff.], such reverse order should be used on the counter board-abecedarium in order to receive numbers consisting of components written in the regular order, i.e. senior categories on the left, and junior ones – on the right.
Greeks copied the system of alphabetic record of numbers from Egyptians (who fixed it in hieratic and demotic scripts). The principle of this system was that for each kind of units (from 1 to 9) there existed an ennead (a nonary, in Greek) of signs, an ennead of other signs – for tens (from 10 to 90), two different enneads for hundreds (from 100 to 900) and thousands (from 1000 to 9000). In Egypt special signs were used for recording numbers only, which were not applied for recording sounds. Greeks, unlike Egyptians, used their alphabet for this purpose, i.e. the letters applied for recording sounds, as well. In early-Greek period including the VII century BC, many Greek cities-states had their own alphabets. There are many grounds to suppose that Greeks also used their local alphabet for recording numbers. Table 1 gives possible values of numbers written by letters of the Euboean alphabet.
I do not insist on 100 % validity of the possible numerical values of letters on the Marsiliana tablet written in Table 1. Apparently, further researches of texts written in the Euboean alphabet and including records of numbers, will allow us to specify some details.
Later, in 403 BC, a unification of the Greek alphabet was made in Athens. To record numbers, the Greeks used their alphabet (24 signs) and three out-of-date letters (episems) – totally, 27 signs, i.e. three enneads – for units, tens and hundreds. In Table 2, signs of the unified Greek numerical alphabet (so-called Ionic system of numeration) are presented.
I do not dwell on minor details of recording numbers (for example, to distinguish numbers from a verbal text, a horizontal line was drawn above all letters of a number; there were special methods of recording numbers equal to units of thousand, etc.). This is described in detail in literature [See for example, Heath, 1921, I]. By the way, Greeks in those days already wrote from left to right, and numbers were written in a manner accepted as early as in ancient Babylon. Then, signs of addition and subtraction (our + and -) did not exist yet, and summands were written immediately one after another. If the left item was greater than the right one, such numbers were summed up. If, on the contrary, the left item was smaller than the right one, such left number was subtracted from the right one, and the result was perceived as a difference. We are well aware of it by later Roman numbers: IX = 9, XL = 40, XC = 90. Therefore, to write a number as a sum of components, it was necessary to place the greatest component on the left, and smaller ones – to the right. And since any ten is greater than any unit, and any hundred is greater than any ten, there was a rule: to write first (on the left) hundreds, then tens, and then – units.
To record a number is a half-battle. How could they add and subtract numbers written in this way? For this purpose, there was a counter board (abacus-abecedarium). The scheme of the counting on the abacus-abecedarium as applied to the Ionic alphabetic numerical system is shown in Fig. 2. Components of numbers were marked by stones (psephoses, in Greek). In this figure an example of the addition of two numbers is shown. The main principle of addition is that stones of units should be added to stones of units, stones of tens – add to tens, stones of hundreds – to hundreds. At the addition of one stone of units to the existing stones of units, the stone of the result is moved to the left by one position. If the quantity of stones of units exceeded nine (θ), all stones of units were removed from the board and replaced with one stone of tens added to stones of tens. The same principle is applied for tens and hundreds. And on the contrary, at the subtraction, if it is necessary to subtract a unit, and the minuend does not have stones in the category of units, then one ten is borrowed the category of tens (i.e. the stone of tens is moved to the right by one position), the unit is subtracted from this borrowed ten, and the remaining nine units are placed into the result (to the position θ).
We can assume with confidence that the above-described system of counting by means of counting board-abecedarium was not thought up by Greeks, but copied from an Egyptian analogue. The Marsiliana tablet points to it. Its manufacture from ivory, use of wax for recording components of numbers (instead of using a stone-psephos, a calculator made a pit in wax with a style in a respective place, and instead of moving the psephos, smoothed out the initial pit with a spatula on the opposite end of the style and made a new pit in the necessary place) and other attributes show that it was a serial product, and not a "pre-production model".
Egyptians applied a method using addition of doubled components (details are described in literature [Gillings, 1972]) for multiplication.
Thus, already in the VII century BC, the Greeks had their “palmtop computer”. That is the way the Marsiliana tablet may be considered.
The author is grateful to Natalia Goldbaum for help in the preparation of this article.
References
Buonamici, G., 1932, Epigrafia Etrusca. Florence.
Gillings R.J. , 1972, Mathematics in the Time of Pharaohs. Cambridge, Mass.
Heath T.L. , 1921, History of Greek Mathematics, Oxford, Clarendon Press, vol.I.
Jeffery, L.H., 1961, The Local Scripts of Archaic Greece. Oxford: Clarendon Press.
Minto, A., 1921, Marsigliana d’Albegna. Firenze.
Von Vacano, O.-W., 1960, The Etruscans in the Ancient World. London.
Nemirovsky A.I., 1983. Etruscans (from myth to history), Moscow, Nauka, (Russian).
(Немировский А.И., 1983, Этруски (от мифа к истории), Москва, Наука).
Tsayger M.A. , 2007, Arithmetic among the ancient Slavs and in pre-Petrine Russia, Voprosy Istorii Estestvoznanija i Tehniki, № 2, (Russian).
(Цайгер М.А., 2007, Арифметика у древних славян и в допетровской России, ВИЕТ, № 2)
Table 1. Possible numerical values of letters on the Marsiliana tablet

Table 2. The Greek (Ionic) numerical alphabet
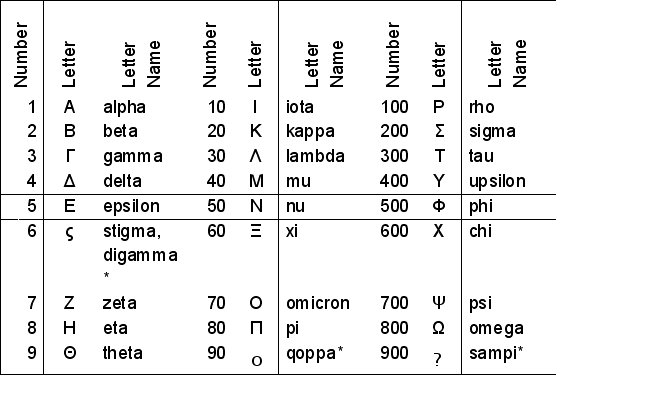 Note: *out-of-date letters (episems) used only for the designation of numerical values.
Note: *out-of-date letters (episems) used only for the designation of numerical values.
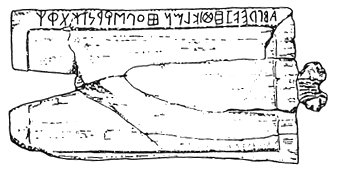 Fig.1. The Marsiliana tablet (c. 700 BC)3 . Its sizes are 2 inches x 31/2inches (51 mm x 89 mm).
Fig.1. The Marsiliana tablet (c. 700 BC)3 . Its sizes are 2 inches x 31/2inches (51 mm x 89 mm). The internal rectangular area was filled with a layer of wax whose traces remained.
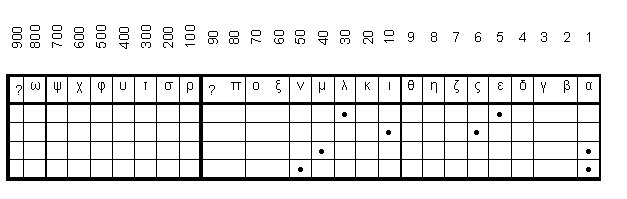 Fig.2. Addition of two numbers on a Greek counting board-abecedarium: λε + ις (35 + 16).
Fig.2. Addition of two numbers on a Greek counting board-abecedarium: λε + ις (35 + 16). In the first line – the first item (λε), in the second line – the second item (ις).
In the third line - units from the second item (ς) are added to the units of the first item (intermediate result - μα).
In the fourth line – tens of second item (ι) are added to the intermediate result. The final result - να (51).
1 Now the Ischia island.
2 Abecedarium is the sequence of the letters which have been written down in alphabetic order.
3 Figure from page 1, The university of Oklahoma, Classes online, Etruscan Art, Language,
(http://www.ou.edu/class/ahi4163/slides3/alphabet.gif)







