Уважаемые коллеги!

Хотя Электрон Добрускин вполне реализовал себя,  прожив долгую насыщенную жизнь, все равно бесконечно жаль, что его больше нет.

Я был знаком с ним только заочно. Но он проявил живой интерес к моим работам и способствовал их появлению на ЭНС, относясь к ним доброжелательно, но и критично.

Я, как и многие, встал на путь безвозмездной публикации идей для всеобщего сведения и блага, но он этим не ограничился, а стал организатором и вдохновителем широкого общения между всеми нами. Вечная ему благодарность и память.

И, я согласен, пусть главным памятником ему будет растущий и крепнущий ЭНС.

И тут я хочу провозгласить приоритетность направления, связанного с когнитивной эргономичностью фундаментальных и прикладных наук.

Одним из первых (еще не зная самого термина) о нем писал И.М.Сеченов: <Кратчайший путь к истине обычно находят много позже того, как она обнаружена долгим и трудным окольным путем> (слегка перефразировано).

Образно выражаясь, ухабистый окольный путь нужно заменить прямой, короткой и гладкой дорогой, а заодно расставить недостающие указатели.

Такая оптимизация изложения –  необходимый элемент познания, даже если она не вносит новой информации. Но на самом деле она ее всегда вносит.

ЕЩЕ РАЗ ОБ ЭРГОНОМИЗАЦИИ.

СТРАСТИ ПО ТЕРМОДИНАМИКЕ.

Часть 2.

А.Б.Шур

Условные обозначения и сокращения.

T – абсолютная температура,

p – давление,

V – объем,

Q – теплота,

A – работа,

U – внутренняя энергия,

H – энтальпия, или теплосодержание при постоянном давлении

S – энтропия,

F – изохорно-изотермический потенциал (свободная энергия), 

G – изобарно-изотермический потенциал (энергия Гиббса),

h – КПД термодинамических циклов,

L – скрытая теплота превращения (плавления, испарения, перекристаллизации),   

G  –  нулевой верхний индекс – признак стандартного состояния,

Kp – Константа равновесия реакции,

R –  универсальная газовая постоянная,

ТТ, ХТ – техническая и химическая термодинамика,

ДУГГ – дифференциальное уравнение Гиббса-Гельмгольца,

ИзхИП,  ИзбИП, ИИП – изохорно-изотермический и изобарно-изотермический потенциалы.     

Внимание!  Нумерация рисунков сквозная с частью 1.

Незапланированное предисловие.  

Ряд личных проблем задержал редактирование этой статьи. Досадная задержка неожиданно пошла на пользу: я смог познакомиться с выступлением [1]  и отреагировать на него. Вроде бы речь о другом, а на самом деле – о том же самом, лишь в другом ключе и с другими акцентами. Ограничусь минимумом пояснений.

Известно, сколь много времени и усилий занимает написание статей об уже сделанном и понятом для себя, если цель – не просто застолбить, а донести мысли до других. То же самое – подготовка учебного пособия или лекционного курса.

В.Демидов [1] http://www.elektron2000.com/article/1401.html для показа, почему так, анализирует право-левополушарные связи. Вот введение в проблемы когнитивной эргономики, задолго до ее появления.  “Сцепление понятий в уме бывает иногда столь тонко, столь нежно, что малейшее покушение обнаружить сию связь словами разрывает ее и уничтожает... ”  (М.М.Сперанский, 1795 – цитировано в [1]).

Не считая возможным далее входить в подробности выступления, обращаю на него внимание читателей. От себя добавлю еще ссылку на Ф.И.Тютчева: “мысль изреченная есть ложь”.

Замаскированные ловушки.

Привычное глубокое заблуждение – сводить трудности термодинамики к математическим. Как раз математика в ней предельно проста, а главные трудности – смысловые. Нет здесь и безумных идей, в отличие от теории относительности или квантовой механике.

Первенство в роли затруднителя держит  та же причина, что вызывает смех в анекдотах и каламбурах. Их “соль” – употребление одних и тех же слов для обозначения совершенно разных вещей, и создание затруднений различению контекста. Классический пример: шли два студента и дождь, один в галошах, другой на лекцию. В каламбуре – смешно, а в обучении –  смысловые ловушки. Отсюда – и пресловутая сложность термодинамики. Этим-то хорошо замаскированным ловушкам я и уделил особое внимание в своем курсе, и им же посвящена эта статья. 

Ветви термодинамики и машиноцентрический перекос.

Техническая термодинамика (ТТ) – теория тепловых машин – возникла и развилась раньше других приложений. Отсюда определенный машиноцентризм в выводах и построениях всей этой науки. Химическая термодинамика (ХТ) возникла позже, и вначале в ней использовали готовые наработки ТТ, а потом появились и специфические для нее понятия. Отсюда, кстати, и сохранившаяся путаница знаков тепловых эффектов – противоположных в ХТ и термохимии.  Это, впрочем, самое безобидное из недоразумений, поскольку с ним все ясно.  Химическая реакция (горение топлива) – источник теплоты. Она для термохимии – целевая функция, и потому положительна, для тепловой же машины цель – работа, а теплота – получаемый извне ресурс, поэтому в ТТ  она положительна, если приходит, и отрицательна – когда уходит.    

Хронология обусловила движение мысли от ТТ к ХТ. Не сразу заметили, что иногда полезен и обратный путь. Привычный порядок изложения надолго сохранился по инерции.

Цикл Карно и второе начало

Главный анахронизм – знакомство с энтропией через цикл Карно. Готовя свой курс, я отказался от этой исторической реликвии и ввел энтропию изначально простейшим путем (о чем уже упоминал, см.     http://www.elektron2000.com/article/1367.html  ).

Ущербность машиноцентризма многолика и хорошо замаскирована. Прежде всего, нелогично формулировать закон природы, как технологическое правило. При создании ТТ речь и не шла о законе природы, интересовались именно технологией.

Хочу сразу отмежеваться от самоуверенных и невежественных ниспровергателей вроде [2],  утверждающих, что принцип Карно устарел вместе с неверной базой. Да, Карно верил в теорию теплорода, и это была его беда. Но,  вопреки ей, он пришел к правильным выводам, заложил основы второго начала термодинамики, когда еще не было открыто первое (которым он тоже невольно оперировал). Клаузиус и другие развили его идеи, показали их непреходящее значение, очистили от мусора. А разве Гальвани и Вольта, проложившие путь к электротехнике, лучше понимали предмет своих открытий? Ученых оценивают по тому, что они сделали, а не по тому, чего они не сделали. Путь к открытию второго начала вряд ли мог быть иным, чем был.

Но сейчас речь о другом. После того, как истина добыта, нужно сделать путь к ней доступным для непосвященных: теория должна быть не только верной, но и эргономичной. А для этого продолжатели должны творчески перерабатывать изложение, а не переписывать из учебника в учебник застывшие формулировки. Процесс эргономизации, однако, застопорился, и не был доведен до логического завершения.

Одна из формулировок второго начала гласит: КПД теплового двигателя не может превысить КПД идеального цикла Карно, составляющего единицу минус отношение абсолютных температур холодильника и нагревателя. Она столь же верна и столь же двусмысленна, как каламбур про студентов и дождь. Ведь сама формула следует из первого, а вовсе не из второго начала (как все формулы теплоты и работы, а значит и КПД, для любого цикла). Отсюда – одна из тех самых ловушек и недоуменный вопрос. Так независимо второе начало от первого или выводится  из него?

А секрет прост, хотя и скрыт. Формула-то получена из первого начала, но суть второго начала вовсе не в ней, а в знаке неравенства (который здесь подразумевается), да и то не всегда.  Почему не всегда – сейчас увидим, а пока замечу, что авторы книг по термодинамике привычно включают описание цикла Карно в раздел “Второе начало”, что уже и само по себе провоцирует непонимание. Этой методической ловушки не избежал и великий Г.Лоренц [3].

Я ликвидировал ее и сделал прозрачным вопрос о происхождении цикла Карно. Для этого ввел его и рассчитал КПД заранее, в разделе о первом начале, и отложил “на потом” все разговоры о его связи со вторым началом. А после введения понятия энтропии вернулся к нему и показал (не я первый, разумеется), что в координатах T – S расчет кардинально упрощается по сравнению с координатами p – V.  Изотермы превращаются в горизонтали, адиабаты – в вертикали, а все изображение цикла – в прямоугольник, при одном лишь взгляде на который (см. рис.3, справа)  становится ясен и результат, и то, почему этот 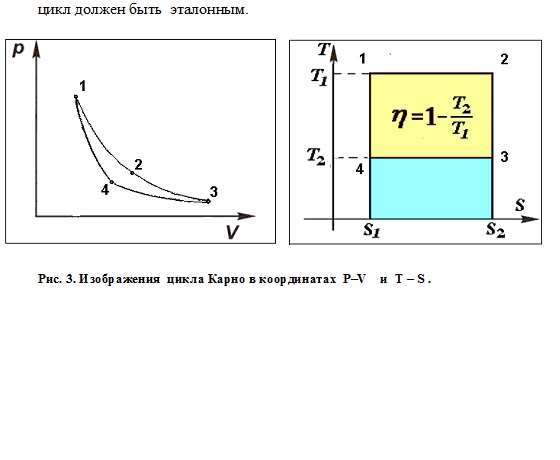 Его КПД – наибольший среди всех обратимых циклов между заданными температурами просто потому, что любая фигура, вписанная в прямоугольник, меньше его по площади. А поскольку о втором начале речи еще не было, то знак неравенства и не относится к нему (напомню, было обещано показать, почему не всегда он связан со 2-м началом). 

Со вторым же началом этот знак связывают два обстоятельства.

Во-первых, то, что отвергается гипотеза о возможной зависимости КПД от вида рабочего тела. Именно Карно впервые постулировал, что замена идеального газа некой другой субстанцией тут ничего изменить не может.

Во-вторых, любой цикл, и Карно в том числе, можно провести обратимо или необратимо (слово можно, разумеется, чистая условность). Необратимость возникает в реальном цикле по причине потерь на теплопроводность и излучение, на трение в сочленениях движущихся частей, на неплотности  прилегания цилиндра и поршня. Другими словами, любой цикл “может” быть реальным или идеальным, а цикл Карно, кроме того, “самый” идеальный среди всех идеальных.

Знак неравенства “меньше или равно” в формуле КПД (вместо знака равенства), учитывающий эти обстоятельства, как раз и дает математическую формулировку второго начала. Но она, как видим, неоднозначна – в духе того самого каламбура. 

От всех этих двусмысленностей свободна общая математическая формулировка второго начала (рис. 4, 5).  Ниспровергатели [2] считают энтропию бессмысленной  выдумкой Клаузиуса, ничего не означающей и не приносящей никакой пользы. Да, она абстрактна, но что поделаешь – абстракция есть необходимый инструмент в науке. Здесь она делает однозначной математическую формулировку, которая всегда и безоговорочно относится к сути второго начала.  К ее выводу и использованию мы еще вернемся. Замечу, что в учебнике [5] обошлись совсем без цикла Карно, и достаточно логично, но все же  сложновато для первого чтения ввели энтропию.   

А пока напомним, что содержательных формулировок второго начала  известно несколько, и любую из них можно принять за аксиому, а остальные вывести из нее, как теоремы. Выбор между ними – вопрос эргономический. Из них наиболее популярны две.

Постулат Клаузиуса: Невозможен процесс, единственным результатом которого являлась бы передача тепла от более холодного тела к более горячему.

Постулат Томсона (Кельвина): Невозможен круговой процесс, единственным результатом которого было бы производство работы за счет охлаждения теплового резервуара.

Оба эквивалентны абстрактной формулировке через энтропию. 

Цикл Карно и рядовой потребитель

Перестав быть истоком теории, цикл Карно остается эталоном и путеводной звездой при проектировании всевозможных машин, и в этом качестве интересен как для специалистов, так и для потребителей.   

Начнем с автомобилистов. Характеристики двигателя во многом определяются сравнением индикаторных диаграмм с таковыми для цикла Карно. Существует даже термин карнотизация – приближение к эталонному циклу.

И это при том, что сам двигатель Карно практически неосуществим. Он предусматривает такие степени сжатия, каких не выдержит ни один реальный мотор,  а если усилить конструкции, то не выдержит никакая экономика. И, тем не менее, преимущества дизельного двигателя перед карбюраторным определяются именно степенью карнотизации.

Небольшой ликбез о холодильном цикле. Это – обратный цикл (просьба не путать с обратимостью), на диаграмме – против часовой стрелки. Допустим, холодильник стоит в помещении с температурой 25 градусов (298 К), и в нем поддерживается температура 0 (273К). На компенсацию потока тепла, идущего внутрь через стенки,  расходуется электроэнергия: (298 – 273)/298 = 25/298 =0.083 кВт/кВт. Вся она превращается в тепло, которое греет комнату (то и другое измеряем в одинаковых единицах).

Вывернув холодильник так, что тепло выкачивается из комнаты наружу,  получаем тепловой насос –  кондиционер, работающий на охлаждение.  Обратив направление потока, получаем кондиционер – отопитель. При тех же температурах – нулевой  на улице и 25 в комнате – получаем  298/(298 – 273)=298/25 =12 кВт тепла на 1 кВт затраченной мощности. И это – вместо 1 кВт/кВт у простого нагревателя.

Многие ли владельцы холодильников и кондиционеров ясно представляют себе эту арифметику?  Помню газетную шумиху в Москве, лет 40 или 50 назад, о великом достижении специалистов некоего завода, сумевших нарушить не только второе, но и первое начало термодинамики. На самом деле, с термодинамикой  все в порядке, ее просто нужно правильно понимать. Электроэнергия превращается в теплоту в соотношении 1 к 1, но для электроплитки на этом все и заканчивается, а в тепловом насосе, кроме того, теплота перекачивается с нижнего на верхний уровень без всякого преобразования.

Заметим одно существенное различие между прямым и обратным циклами. Эффективность двигателей возрастает с увеличением разности температур между верхним и нижним уровнями. Эффективность тепловых насосов, наоборот, возрастает с уменьшением этой разности.

Известно, что в Швеции тепловые насосы, использующие теплоту морской воды для отопления, распространились очень широко. Для таких стран, как Украина или Израиль, это направление весьма перспективно. Не последнюю роль в отставании тут играет степень информированности (точнее, неинформированности). Чтобы пользоваться плодами науки, о них должны знать не только специалисты, но и все остальные – предприниматели, чиновники депутаты, и их избиратели.  Сейчас, правда, о тепловых насосах уже можно почитать в рекламе интернета.

Не только изолированная система

Вернемся к общей теории. Напомню, закон роста энтропии справедлив только для изолированных систем, но нас интересуют не только они, и даже в первую очередь не они. Выше упоминалась и общая формулировка, но без ее вывода. Восполним этот пробел. На рис. 4 показан простейший переход от изолированных систем к общему случаю.

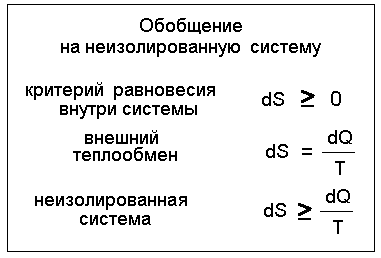
Рис.4.

 Обобщение математической формулировки второго начала

Сложение формул изменения энтропии при внешнем и внутреннем теплообмене для заданной системы (равенства и неравенства) дает суммарный результат, верный для любых процессов. Принято, что внешний теплообмен обратим, а все возможные необратимости относятся только к внутреннему теплообмену. Это не нарушает общности вывода: если допустить, что возможна и необратимость внешнего теплообмена, то результат справедлив тем более.

А теперь настал момент вернуться к Я.Б.Зельдовичу (сначала пойми, а строгость –  на потом) и покаяться в допущенных прегрешениях.

Сеанс черной магии с ее разоблачением.  

Все предыдущее, включая часть 1, понятнее вывода Клаузиуса, но содержит одно преднамеренное упущение. Не указано, что энтропия есть функция состояния (а не процесса, как теплота и работа). Чем оно вызвано?

У Клаузиуса в центре внимания именно это доказательство, но в  эргономическом смысле – он нарушил пожелание  не накладывать трудность на трудность (второе правило Василевского). А именно, не разделил два сложных для понимания тезиса: 1) энтропия есть функция состояния, 2) она же – мера необратимости.  

Я отделил одну трудность от другой и пришел ко второму тезису простейшим образом (часть 1, рис.1). Но первый тезис при этом выпал! Тем самым, диаграмма в координатах T – S (рис. 3) введена, пока что, незаконно. Я старался вначале давать только самое необходимое  (третье правило Василевского). Читатель мог этого и не заметить, но долги нужно отдавать.

Простейший путь отдать этот долг  –  нарушить хронологию открытий,  и,  перед развертыванием следствий из первых двух начал, сразу ввести   третье начало термодинамики. Оно позволяет получать абсолютные значения энтропий для любых веществ и при любых температурах. А это и доказывает, что энтропия есть функция состояния. Без всяких машин и циклов, и без одновременного доказывания других трудно постижимых истин. Такой отказ от следования хронологии дает и другие, не менее важные преимущества.

Третье начало и абсолютные энтропии

Два первых начала – законы дифференциальные. Для перехода к интегральным соотношениям необходимо знать постоянные интегрирования или способы их получения. Недостающие константы и дает третье начало, первоначально известное, как тепловая теорема Нернста (1911 г.). Оно гласит, что с приближением температуры  к абсолютному нулю, теплоемкости и энтропии всех веществ также стремятся к нулю. Его называют еще законом недостижимости абсолютного нуля температур. Будучи изначально обобщением экспериментов, он впоследствии был обоснован квантовой механикой, чего мы касаться не будем.

    Расчет абсолютных энтропий достаточно прост –  это формула 1 в таблице 1.  Но при нулевой температуре эта формула дает бесконечность, если не учитывать третье начало, которое от нее избавляет. Единственное, что требуется знать – температурный ход теплоемкости от абсолютного нуля до заданной температуры.

Формула 1 была бы достаточна, не будь фазовых превращений  – плавления, испарения и аллотропических преобразований. Каждое такое превращение дает добавку энтропии согласно формуле 2 той же таблицы.  Одновременно и сам интеграл распадается на несколько однотипных формул вида 1, с подстановкой для каждой фазы своего интервала температур и своей теплоемкости. Эти формулы чередуются с формулами вида 2, каждая со своей температурой и теплотой превращения. Теплоемкости задаются степенными рядами из 2 - 4 членов, коэффициенты которых приводятся в справочниках физико-химических величин. 

Одно необходимое пояснение. Формулы 1 и 2 массовому пользователю на самом деле не нужны, и показаны здесь лишь для знакомства с принципами.  Все расчеты по ним проделали составители справочных таблиц, где даны абсолютные значения энтропий (обозначение 3 в таблице 1). Нижний индекс – температура, для которой рассчитано значение. Это обычная комнатная температура 25 градусов С, или 298 К.

Верхний нулик показывает, что значения приведены для стандартного состояния,  которое для твердых веществ означает правильно образованные кристаллы без примесей, для жидкостей – отсутствие растворенных веществ, для газов – парциальное давление в 1 физическую атмосферу. В выражение энтропии для газов добавляется еще зависимость от давления (4, 5, 6). Значение с верхним нуликом есть стандартное значение энтропии при давлении в 1 ат, для которого логарифм равен нулю. В системе СИ все неоправданно усложняется, поэтому применяю «устаревшие» единицы давления. Кому потребуется, разберется.

Пользователю остается учесть разницу между реальными и табличными условиями. Заметим, что учет влияния давления для газов на данном этапе кажется мелким уточнением, которым можно бы и пренебречь. Но перейдя к расчетам равновесий, мы увидим, что именно формулы 4-6, учитывающие указанное влияние, и есть главная содержательная основа, на которой они базируются.

Теперь можно вернуться ко второму началу.

Три лика одного закона.

Универсальное выражение математической формулировки второго начала хорошо своей краткостью, но для непосредственного пользования неудобно, тут желательна конкретизация. Для трех самых интересных случаев оно  распадается на три  простых выражения (рис. 5).  

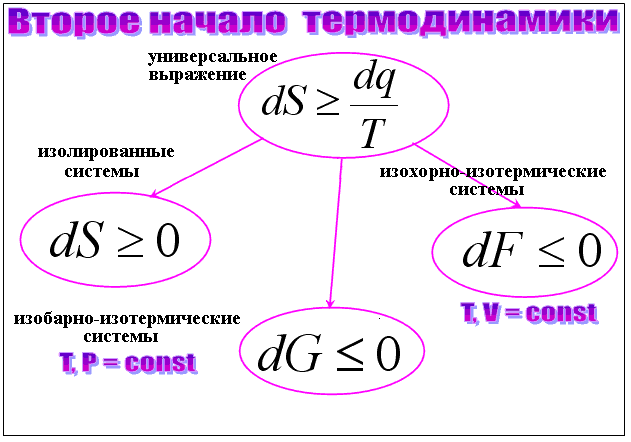
 Рис. 5. Общее и частные выражения второго начала термодинамики.

Первое из них  –  уже известный нам вариант для изолированных систем, где отсутствует внешний теплообмен; 

второе – вариант для изохорно-изотермических систем, где постоянны температура и объем;

третье – для изобарно-изотермических систем, где постоянны температура и давление.  Это – наиболее употребительный вариант, и дальше речь пойдет преимущественно о нем.

Здесь F = U – T*S – изохорно-изотермический потенциал (ИзхИП), или свободная энергия;

G = H – T*S = F+ p*V – изобарно-изотермический потенциал (ИзбИП), или энергия Гиббса (разновидность свободной энергии);   

H = U + p*V – энтальпия, или теплосодержание при постоянном давлении.

Что такое свободная энергия и что такое хороший учитель.

Чтобы без большого напряжения пояснить смысл свободной энергии,  вернусь к студенческим годам и воспользуюсь блестящим примером педагогического мастерства, которое проявил наш лектор по курсу воздуходувных машин (каюсь – забыл фамилию).  Однажды, по ходу лекции,  он предложил нам такую задачку.

Стальной баллон накачали сжатым воздухом и хранили на складе. Подключив к нему турбинку,  совершили работу – например, подняли груз. Спрашивается: откуда и каким путем черпалась энергия для этой работы (считая  процессы сжатия и расширения изотермичными)? Естественно, мы хором ответили: конечно, от компрессора, которым накачали баллон! Тогда последовал второй вопрос. Так Вы считаете, что энергия все это время хранилась в баллоне?  Ответ: конечно! Тогда третий вопрос. От чего зависит внутренняя энергия идеального газа? Ответ: от температуры, и больше ни от чего. Но ведь температура воздуха, а значит и его внутренняя энергия до сжатия и после хранения  была одна и та же!  

А значит, на первые два вопроса мы ответили неверно. Вся работа, совершенная компрессором, перешла в тепло, унесенное охлаждающей водой. А энергия для работы, совершаемой турбинкой, поступает снаружи. Что же изменилось в газе при его сжатии с точки зрения энергетической? Возросла его свободная энергия за счет сокращения энтропии (точнее, связанной энергии, равной произведению T*S). Газ приобрел способность черпать энергию из тепла окружающей среды.  

Если бы сжатие было адиабатическим, работа перешла бы во внутреннюю энергию газа, и если дать ему расшириться сразу после этого, то он совершил бы ту же самую работу (большую, чем в изотермическом случае), и тогда (и только тогда) наш ответ был бы верен. Если же дать баллону остыть, то при последующем адиабатическом расширении он охладится до еще более низкой температуры. Полученная при этом работа будет меньше, чем ее затрачено при сжатии – процесс окажется необратим. А необратимыми его звеньями будут охлаждение после сжатия и нагрев после расширения.

Замечание. В условиях этого мысленного опыта ИзхИП и ИзбИП равны между собой, так что безразлично, к какому из них относить сказанное.

Разумеется, все эти сведения содержались в уже прослушанных нами курсах физики, физической химии, технической термодинамики. Но содержались в латентной форме, и с полной ясностью дошли до меня только после этого эпизода и размышлений по его поводу. У преподавателей тех курсов было куда  больше оснований прояснить этот вопрос, но сделал это представитель прикладного курса, лишь косвенно к нему причастный. Для понимания не только его, но и всей термодинамики, тот случай оказался более значим, чем прежние лекции, прямо к нему относившиеся. Став сам преподавателем, я неоднократно задавал его студентам, а заодно и коллегам, и описанный сценарий неизменно повторялся.

Наш лектор правильно определил слабое место, требующее подстраховки. Фундаментализация образования требует встречного движения в фундаментальных и прикладных курсах. Это – тот самый случай: преподаватель-прикладник сработал на фундаментализацию знаний, и отнюдь не в ущерб своей основной задаче, затратив на это каких-нибудь 5 минут. 

Веревка и муравей 

А сейчас мне нужно перейти, наконец, к главной цели ХТ – исследованию химических равновесий, и показать те несколько сосен, между которыми я блуждал столько лет (а многие продолжают блуждать). Начну с пояснений на пальцах (рис. 6). Ограничусь только изобарно-изотермическим случаем, наиболее важным для реальных технологических процессов. ИзбИП – это весьма абстрактная характеристическая функция, позволяющая судить об ожидаемом направлении процесса при постоянных температуре и давлении. Представьте провисшую веревку, концы которой у Вас в руках. Примем ее за подобие графика функции в зависимости от прохождения реакции.

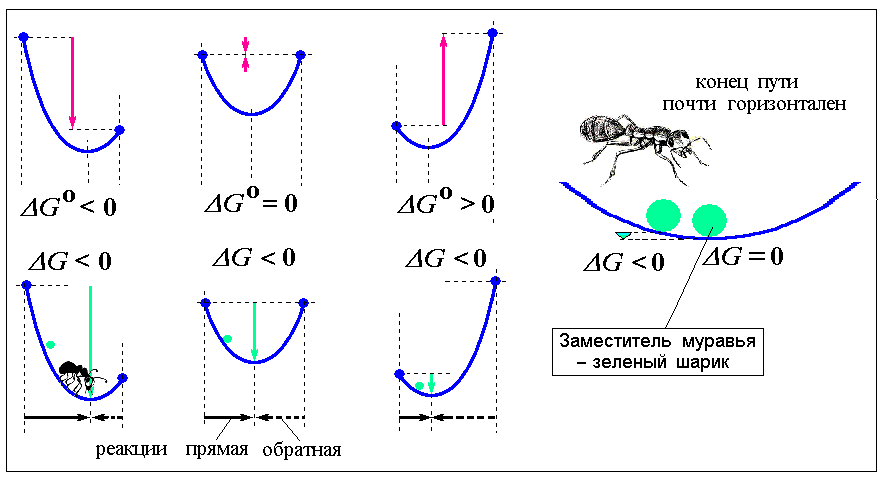
Рис.6. Как меняется изобарно-изотермический потенциал по ходу реакции

По веревке ползет муравей. Вообразим, что он знает, в какую сторону идет химическая реакция, и ползет именно туда. Так вот, ползти вверх ему запрещает второе начало термодинамики. Он может начать движение хоть справа, хоть слева, но остановится в самой нижней точке.  (На рисунках заместителем муравья показан зеленый шарик)

Если держать концы веревки на одном уровне, то нижняя точка окажется как раз посередине. Если правый конец поднять, то минимум сместится влево, а если поднять левый –  сместится вправо.  Для удобства, эти три положения веревки показаны два раза, в верхней и нижней частях рис. 6.

Слева реакция еще не начиналась (одни начальные вещества), а справа она уже завершилась (остались только конечные продукты). Рассуждение годится и для обратной реакции – нужно просто правый конец  поменять с левым. На самом деле, реакция не может пройти полностью в одну сторону. С какого бы конца ее ни начать, она остановится в той самой нижней точке. Минимум ИзбИП –  признак равновесия.

Нужно понять разницу между  величинами G  и G^o. Верхний нолик означает значение ИзбИП для стандартного состояния. Что это такое – было сказано выше применительно к энтропии. Для химической реакции величина ΔG^o означает изменение, происходящее при переходе чистых исходных веществ в стандартном состоянии в чистые конечные вещества, тоже в стандартном состоянии (показано в верхней части рисунка красными стрелками).  Величина ΔG (без нулика) относится к изменениям в реальных процессах при переходе от исходных веществ, либо другого исходного состояния, к равновесной смеси (показано в нижней части рисунка зелеными стрелками).

Так вот, разность уровней Ваших рук – это стандартное изменение ИзбИП, которое на самом деле никогда произойти не может, а действительные его изменения – те, которые проходит наш муравей. Когда он подползает к нижней точке, его уровень практически больше не меняется. Можно поднять вверх правую руку –  стандартное изменение станет положительным, опустить ее вниз – оно станет отрицательным, но в любом случае на последних миллиметрах движения к нижней точке муравей ползет практически по горизонтали. Это и есть условие равновесия:  ΔG =0.

На рис.6 разные положения муравя показаны зелеными шариками. Концы веревки обозначены синими шариками – это стандартные значения для исходных и конечных веществ. Красные стрелки – стандартное изменение ИзбИП, а зеленые стрелки – фактическое его изменение при переходе к равновесию.

По ходу реакции ИзбИП всегда уменьшается. В точке равновесия его изменение при малом продвижении равно нулю, а дальше он стал бы возрастать, но это невозможно. Итак, равенство нулю изменения ИзбИП – это признак равновесия. А равенство нулю его стандартного изменения – это признак того, что равновесие наступит посередине нашего интервала. Но для верхоглядов различия между этими совершенно разными вещами не существует. То есть, они путают зеленые и красные стрелки.

В их оправдание можно сказать, что вопрос, действительно, достаточно запутан и труден. А трудность – от того, что обе величины обозначены почти одинаково. Вся разница – верхний нолик. При этом еще величина без нолика есть критерий равновесия, а величина с ноликом –  ключевой пункт для расчета константы равновесия. А именно:

       ΔG =0  –  условие равновесия,

ΔG^o = –RTlnKp  – выражение для расчета константы равновесия.

     Считать ΔG^o =0  условием  равновесия – грубейшая ошибка (за исключением случая, когда реальные условия совпадают со стандартными).

Константа равновесия рассчитывается через величину, которая никогда не реализуется. Есть повод для того, чтобы поехала крыша!

Как я сменил специализацию.

Когда-то я и сам был таким же верхоглядом. Начало излечению положил М.М.Карнаухов, читавший нам курс металлургии стали. Обнаружив эту путаницу в журнальной статье за подписью большого научного начальника, он продемонстрировал ее нам с изрядной долей сарказма. О веревке и муравье речи не было, это мое более позднее изобретение. Разумеется, веревка – это не объяснение, а только намек и мнемонический прием, чтобы уловить хотя бы внешнюю оболочку событий.

Как оказалось, тех же заблуждений, что и автор злополучной статьи, придерживался мой шеф, лектор курса электрометаллургии стали и ферросплавов, следующего за карнауховским.  Хотя я тогда еще не вполне разобрался в вопросе (еще ведь не была извлечена первая заноза!), все же сумел заметить, что концы с концами не сходятся, и начал задавать вопросы. Когда до него дошло, к чему я клоню, он страшно на меня обиделся. Этим, в конце концов, определился и окончательный выбор мною специальности. Я с самого начала ориентировался на электрометаллургию стали. Но после ссоры с шефом вспомнил, что меня давно уговаривали специализироваться по металлургии чугуна. И согласился. Так, вопреки своим прежним планам, я стал доменщиком.

Итак, очередная (но не последняя) заноза состояла в неумении различать красные и зеленые стрелки на рис. 6. На занятиях по сталеплавильным дисциплинам было лишь положено начало ее извлечению, а окончательно я от нее  избавился много позже, составляя свой собственный учебный курс.

Как просто ларчик открывался!

Константа равновесия – это дробь, числитель которой (упрощенно) есть произведение равновесных парциальных давлений конечных продуктов реакции, а знаменатель – то же для исходных веществ. Первоначально ее определяли как отношение скоростей прямой и обратной реакций. Но такое определение выходит за рамки термодинамики – она занимается только равновесиями, среди ее параметров нет понятия времени и никаких скоростей. Ими занимается кинетика – другой раздел физической химии.

 В термодинамических расчетах равновесий используются только термохимические характеристики веществ, и не используются ни экспериментальные данные по равновесиям, ни кинетические параметры. До теоремы Нернста полностью термодинамический расчет был невозможен. Наибольшим достижением той эпохи  (1875) было дифференциальное уравнение Гиббса-Гельмгольца (ДУГГ). Но для его решения недоставало знания начальных условий. Как паллиативное решение, для некоторой температуры проводился как бы калибровочный эксперимент, после чего для других температур открывалась возможность теоретического расчета.

С появлением теоремы Нернста (1911) надобность в этом отпала, и стал возможен чисто теоретический термодинамический расчет. Наиболее полное и ясное воплощение этой возможности – расчет по методу Темкина-Шварцмана (МТШ) [6].  Мое окончательное прозрение произошло именно при осмысливании МТШ,   и   состояло   оно  в  том,  что  теперь не нужен не только калибровочный эксперимент, но и вообще отпала надобность решать ДУГГ!  В самом деле, ДУГГ для постоянного давления имеет вид формулы 7 таблицы 2.  Но с учетом (8), оно превращается в (9) и перестает быть дифференциальным уравнением. Входящее в него стандартное изменение энтропии реакции теперь вычисляется просто, как разность энтропий конечных и начальных веществ.

Остается преобразовать его в формулу для расчета константы равновесия (10, 11).  Вот тут и пригодился учет влияния давления на энтропию газов (формулы 5, 6 таблицы 1).

Вся умственная эквилибристика, вынуждавшаяся отсутствием начальных условий, оказывается попросту не нужной, оставаясь лишь исторической реликвией, показанной в формуле 12 таблицы 2.  В учебнике и учебном курсе ее можно опустить, перейдя после второго начала сразу к третьему началу и следующему из него простому и полноценному  расчету. (Умный в гору не пойдет, он ее обойдет!).

Но почему так долго?

Между открытиями Гиббса-Гельмгольца и Нернста прошло 36 лет, что вполне объяснимо. Но то, что между теоремой Нернста и появлением  МТШ прошло еще 37 лет – кажется невероятным. Это ведь не теория относительности и не квантовая механика, а простенькие интегралы.

Начало застою положил сам Нернст. Преодолев главный барьер, он спасовал перед простыми техническими трудностями и не заметил, что прямой путь уже открыт. Он начал создавать метод расчета через так называемые химические постоянные, и завел в эту трясину целые поколения последующих авторов учебников и студентов.

Согласно остроумному лозунгу Р.Хэмминга, цель расчетов – не числа, а понимание. Цель расчета через химические постоянные – только числа, да и то не всегда верные. Не намного лучше и появившийся позднее метод Г.Улиха.  И лишь в 1948 году метод Темкина-Шварцмана [6] вывел из методологических дебрей расчеты химических равновесий. Он по-настоящему эргономичен, и хорош как раз тем, что дает понимание, а не только числа.  

Казалось бы, осталось пожинать плоды? Ничуть не бывало, вместо этого – очередной парадокс. Авторы учебников [4 и др.] и лекторы вроде бы ничего не заметили, и по традиции продолжают излагать следствия из первых двух начал так, как будто третьего вообще не существует. И лишь потом, основательно измучив читателя и слушателя, показывают ему третье начало и ссылаются на рациональные методы расчета. Создается впечатление – авторы не вполне понимают то, о чем пишут.  В чем же дело?

П.Л.Капица считал главной задачей публикации поставить в нужном месте большой восклицательный знак, и даже числил научный приоритет за тем, кто это сделает первым (заметим: не первый открыл, не первый опубликовал). Так вот: в работе [6] не было того самого восклицательного знака. Авторы не сочли нужным “подать товар лицом”, скромно претендуя  лишь на некоторое усовершенствование безмашинных численных методов. Само название “Вспомогательная таблица для расчетов по химической термодинамике”  создает впечатление чего-то второстепенного. Как же догадаться, что на самом деле здесь целый прорыв в новое качество понимания? Разумеется, этот прорыв связан с самим появлением третьего начала, но ведь оно оказалось недостаточным, и это – та самая недостающая добавка.  

Лично я прозрел именно благодаря этой таблице, но лишь при повторном изучении через 12 лет. Это объяснимо – я еще не был готов. Но воистину удивительно, что идеям МТШ не уделили должного внимания в учебнике [5], один из авторов которого – Л.А.Шварцман. Создается впечатление, что авторы МТШ, подобно Нернсту, сами не поняли того, что совершили.

Снова в Донбассе.

В 1966 году, после защиты кандидатской диссертации, я полностью перешел на преподавание, переехав в Алчевск (тогда Коммунарск) и поступив на работу в КГМИ (ныне ДонГТУ).  

Пришлось вспомнить опыт, приобретенный в Череповце.  Ведя курс ТМП, сразу столкнулся с тем, что студенты не усвоили физическую химию  и не готовы меня понимать (в http://www.elektron2000.com/article/1281.html  уже упоминал об аналогичной ситуации с математикой). Пришлось выделить время на повторение.

Как выяснилось, мой предшественник по чтению курса страдал тем же непониманием разницы между стрелками разного цвета на рис. 6,  что и упомянутый мой бывший шеф по ЛПИ. Он сумел внушить свои взгляды студентам, и мне стоило больших усилий хотя бы некоторых переубедить.

В помощь своим ученикам я сразу написал пособие по ХТ на основе череповецкого конспекта. К сожалению, его не сразу удалось издать. Но все, кому я давал рукопись для пользования, оставались довольны. С появлением виртуальных издательских возможностей, я его доработал и издал, хотя и малым тиражом [7]. Здесь приведена малая часть наиболее характерных оттуда выдержек.  

Я упоминал англо-норвежскую книгу [8] того же замысла – ее перевод появился после создания моей рукописи. Она охватывает более широкий круг вопросов, но в тех, которые для нас общие – считаю, что я решил задачу более основательно и более простыми средствами.

Заключение.

Итак, что в итоге?  Учебники и лекционные курсы термодинамики  остаются,  словами В.Паронджанова,  средствами интеллектуального терроризма.

Прямой путь от теории к расчетам дан лишь в справочниках физико-химических величин /9/,  где много не объяснишь. Усилия по модернизации   направлены по ложному пути внедрения системы единиц СИ, которое в ХТ оказалось наиболее губительным. А то, что вопиет о просветлении – осталось за кадром.  В англоязычной сфере, судя по /8/,  дело обстоит не лучше. 

Я потратил множество усилий, чтобы создать пособие /7/. По 1-2 экземпляра разослал в Публичные библиотеки в СПб, Москве и Киеве,  в СПбГПУ,  МИСиС, Сумской университет,   Технион в Хайфе и др.  

При своих визитах в Израиль в 2009 и 2011, будучи стеснен в средствах на поездки и телефоны, пытался найти место, где бы прочитать лекции на русском языке. Не нашел.

Эта статья – попытка преодолеть трясину непонимания и безразличия и найти заинтересованных читателей, которые захотели бы выйти на кратчайший путь к истине.

Литература.

1.   В.Демидов. Альберт Эйнштейн как личность (философский аспект), http://www.elektron2000.com/article/1401.html  

2. П.И.Дубровский. Размышления о теореме Карно.

http://scicommunity.ru/attachments/article/Дубровсикй%20П.И.%20Размышления%20о%20теореме%20Карно.pdf .

3.  Г.Лоренц. Лекции по термодинамике.

4. В.А.Киреев. Курс физической химии. – М.: ГХИ, 1956. – 832 с.   

5. А.А.Жуховицкий и Л.А.Шварцман. Физическая химия. М. Металлургия 1987,  688 с.  

6. Темкин М.И., Шварцман Л.А.  Вспомогательная таблица для расчетов по химической термодинамике.  Успехи химии, вып. 2, 1948.   

7. А.Б. Шур. Химическая термодинамика в элементарном изложении.

Учебное пособие для студентов,  изд. 2, дополненное и исправленное, Алчевск, ДГМИ, 2002.  Допечатка тиража  Алчевск, ДГМИ, 2004   

8. Д. Тер Хаар, Г. Вергеланд. Элементарная термодинамика  пер. с англ. –  М., Мир, 1968.   Оригинал –   Англия – Норвегия, 1966.     

9. Краткий справочник физико-химических величин, Седьмое издание, под редакцией К.П.Мищенко и А.А. Равделя, Л.: Химия, 1974, 200 с.

Передано автором 11 марта 2017 г.

для обсуждения на семинаре