Выступления по этой статье:
Выступление от 08.07.2014, доктор Хейфец Иосиф, ИзраильВыступление от 24.06.2014, проф Гершанович Исаак, Израиль
Выступление от 21.05.2012, проф. Кузьменко Эдуард, Украина
Выступление от 04.05.2012, академик Шестопалов Вячеслав, Украина
Выступление от 04.01.2012, д-р Бакшт Федор, Россия, канд. геол.-минерал. н. Кузеванов Константин, Россия
Выступление от 09.01.2012, чл.-корр РАН Румынин Вячеслав, Россия
Выступление от 09.01.2012, профессор Красильщиков Леонид, Израиль
- Автор представил ценную работу по попытке решить основную проблему прикладной гидрогеологии – проблему получения достоверных исходных данных малыми средствами. Эта проблема сейчас стала определяющей для дальнейшего развития теории и практики. Статья большая (22 стр). Она не равноценна по своему научному значению. Первая часть статьи носит характер научно-популярной статьи… Самое интересное в статье – автор задумался над "проблемой привести теорию к опыту де-факто, а не наоборот, как это имеет место, т.е. опыт приспосабливают к требованию теории." Для чего надо было, как правильно утверждает автор, пересмотреть природу объекта и найти подход "для связи его с теорией"… Автор набрался смелости сделать новый шаг в исследованиях подземной гидродинамики... Приложения дополняют статью и интересны для профессионалов. Читать полный текст
Леонид Красильщиков
редактор
(в стиле свободного рассказа)
Интрига заголовка относится к науке под названием Подземная Гидродинамика. Ей около 150 лет. Ее рождение связывают с именем Дарси (Henry Darcy). На практике она начала применяться как раздел Гидрогеологии, хотя закон Дарси имеет более широкое применение. Но подлинный расцвет Подземной Гидродинамики как науки и ее практики в Гидрогеологии и Нефтяной Геологии начался с Тейса (Charles Vernon Theis), когда он в 1935 году опубликовал свое фундаментальное уравнение. В последствие, в 40-х годах прошлого столетия, Купер (H.H.Cooper) и Джекоб (C.E.Jacob) модифицировали его до инженерного вида (см. Приложение 1). Это был прорыв в области описания процесса и оценки водо-нефте-проводности горных пород. Хотя Подземная Гидродинамика многое позаимствовала из теории теплопроводности сплошных сред, это не умаляет ее значение. К подземной гидросфере с ее специфическими условиями проведения эксперимента она (теория) выдвигает ряд требований к объекту своего приложения. Это естественно. Любая теория, особенно фундаментальная, исходит из абстракции и нуждается в адаптации. Здесь эта адаптация требовала (и сейчас пока тоже) большие материальные затраты для обеспечения соответствия объекта и данных эксперимента на нем ее теоретическому образу. А не наоборот. Горы статей и книг посвящены этому и много разных модификаций, интерпретаций и аппроксимаций было разработано и издано. Если бы цель была достигнута, не было бы места для этой статьи. Или если бы актуальность проблемы снизилась со временем – то же.
Потребность в подземной воде возрастает по двум причинам: в связи с ростом народонаселения и в связи с ухудшением экологического состояния природной среды. В связи с этим гидрогеология как наука развивалась и развивается по всем своим направлениям, ибо она охватывает, кроме гидродинамики, много других ее составляющих. И соответственно использует достижения смежных наук. Но тема этой статьи, по мнению автора, остается центральной. Это потому, что подземная вода, это единственное полезное ископаемое, которое восполняется в процессе отбора и это происходит путем миграции в пространстве геологической среды. И в ходе этих миграционных процессов она меняет свои свойства, как в лучшую, так и худшую сторону. Следовательно, фильтрационные свойства среды надо уметь определять количественно.
Так как же обстоит сейчас дело с обозначенной темой? Уже к середине 70-х годов прошлого века, когда практическая гидрогеология уже вполне освоила методологию по Тейсу и его модификаторов, а также возможности и преимущества методов математического моделирования для анализа, оценки и прогнозирования гидрогеологических процессов, раздаются голоса неудовлетворенных исследователей. Накипело. Обратимся к авторитетам. В табеле о рангах они заслуживают доверия как равные среди выдающихся ученых в области Подземной Гидродинамики. Вот что они пишут в своей книге (В.А.Мироненко, В.М.Шестаков, 1978, Теория и методы интерпретации опытно-фильтрационных работ, Москва, Недра): «Как и в других науках о Земле, в прикладной гидрогеологии проблема достоверности исходных данных стала сейчас определяющей для дальнейшего гармоничного развития теории и практики. Естественно искать причину низкой точности наших исходных данных в принципах их определения, т.е. в первую очередь в теоретических и методических основах опытно-фильтрационных работ. Отсюда возникают своего рода «ножницы» между возможностями формально-теоретического анализа и грубой схематизацией природной обстановки». Это было как раз время массового применения методологии по Тейсу/Куперу-Джекобу. Для ясности укажу на специфику технологии. Она во всех модификациях требует бурения «куста» наблюдательных пьезометрических скважин вокруг центральной опытной (откачной) скважины на априори выбранном однородном по геологическим признакам участке площади. Почему так? Для не очень осведомленных читателей приведу базовые предпосылки этой теории для ее применения. Приведу основные из них (всего их больше), в переводе на русский.
1. Пласт является однородным, изотропным, выдержанным по мощности и бесконечным в плане
2. Поток к скважине является линейным, горизонтальным и осе симметричным
3. Вода выделяется из пласта мгновенно в соответствии с градиентом напора
4. Пласт является напорным, полностью вскрытым скважиной
5. Скважина имеет малый диаметр, так что ее емкостью можно пренебречь
Можно ли это все выполнить совместно? Как правило, нет. И каков выход? Игнорировать. Что и происходит в действительности. И каковы успехи? «Не легкая это работа из болота тащить бегемота». Наступает время толкователей (интерпретаторов). Постепенно создается «банк» типичных ситуаций и соответствующих им аналитических решений. Это вносит определенную организацию в методологию опытно-фильтрационных работ. Недавно был издан фундаментальный справочник, обобщивший все накопленные к этому времени аналитические модели (Синдаловский Л.Н., 2006, Справочник аналитических решений для интерпретации опытно-фильтрационных опробований, СПб.: Изд-во С.-Петерб. ун-та). Для полноты картины нужно упомянуть, что на основе этого справочника Институт геоэкологии РАН разработал и предлагает на рынке пакет программ ANSDIMAT. Аналогичный пакет под названием Aqtesolv выпускается SWS Hydrogeologic Inc. Canada. Это, хорошо, но мы начинали с того, что озаботились точностью определения параметрических данных и упрощением технологии их получения. В этом смысле и этот справочник, и эти пакеты программ, скорее, памятник, чем маяк. В поисках поддержки сошлюсь еще на авторитетный источник из американской школы гидрогеологов. “Diverse results and vexations will arise if attempts are made to force the application of formulas to aquifer situations differing greatly from ideal conditions” (Walton,W.C. 1983. Selected Analytical Methods for Well and Aquifer Evaluation. Urbana). В моем переводе: «При попытке волевого применения формул к ситуациям, в которых водоносный горизонт существенно отличается от идеальных условий, могут возникнуть неоднозначные результаты и неприятности». Вполне конкретная констатация и предупреждение. Это можно также воспринять как поощрение к ревизии сложившегося порядка вещей с обозначенной целью.
В первом приближении из данных опыта предусматривается получить две базовые величины в уравнении Тейса или его модификациях. Это водопроводимость (transmissivity) и водоотдача (storativity). Все остальные практически полезные характеристики, это производные от этих двух. Оказывается, что и здесь, в суженном варианте, не все благополучно. Обратите внимание на условие «вода выделяется из пласта мгновенно в соответствии с градиентом напора». Это подножка (простите за жаргон). Вода выделяется из пород во время откачки действием двух механизмов: компрессионным и гравитационным. Благодаря снижению порового давления в пласте вода расширяется в объеме и выжимается из порового пространства горным давлением. Это упругая составляющая, а свойство пласта, определяющее ее долю, называется упругоемкостью (specific storativity). Выделившаяся часть объема воды никуда из пласта пока не исчезает. А движется к центру депрессии, т.е. к откачной скважине. Это движение и есть гравитационный поток, так как его движет гравитационная сила по направлению падения давления. Это в так называемых напорных пластах. В безнапорных (грунтовых) пластах то же самое, но еще с частичным осушением. Все это интересно, но нас интересует другое, как выполнить условие «выделяется из пласта мгновенно» части пластовой воды, выделившейся в результате компрессии, образующей поток по уклону, который накладывается на воду, выделяющуюся по ее ходу. Физически это невозможно. Существуют эмпирические рекомендации, как построить опыт, чтобы учесть искажение поля как следствие помех от откачной скважины. Но не это. Это отведено интуиции. Практика – критерий истины. Пример, который приведен ниже, не типичный. Только в исследовательских целях можно было позволить такие затраты. Но они произведены к нашей сейчас радости, и дали нам несокрушимый аргумент.
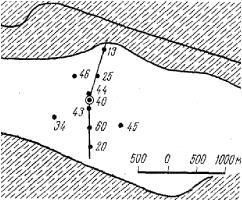
Рис. 27. Куст скважин 40 (сохранена нумерация рисунков авторов).
Все скважины имеют, примерно, одинаковую глубину и конструкцию. Водоносный горизонт представлен известняками и характеризуется как гидравлически безнапорный. Его мощность около 200м. Породы трещиноваты с карстовыми явлениями
Я его позаимствовал из книги пионеров применения и интерпретаторов указанной методологии и вообще авторитетных в прикладной гидрогеологии авторов: (Б.В.Боревский, Б.Г.Самсонов, Л.С.Язвин, 1979, Методика определения параметров водоносных горизонтов по данным откачек. Изд. 2-е, Москва, Недра).
На рисунке показан куст из девяти наблюдательных скважин вокруг опытной скважины №40.Произведена опытная откачка при постоянном дебите продолжительностью около 1000 часов. Все графики временного прослеживания уровня имеют идентичную форму из двух частей: начальной с небольшим наклоном и конечной более крутой. 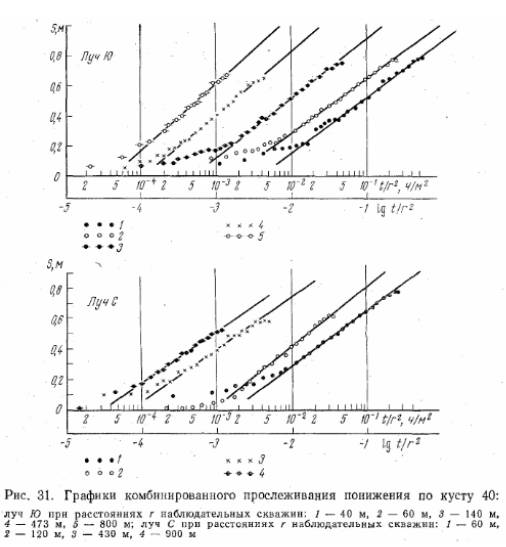
Это типичный случай проявления так называемого эффекта двойной пористости, который проходит со временем, и вся толща пород начинает вести себя как сплошная среда. Этот эффект характеризует инерционность процесса водоотдачи и в действительности сдвигает представительную часть кривых прослеживания уровня по оси времени в сторону больших времен. Причем, чем дальше наблюдательная скважина находится от откачной скважины, тем этот сдвиг по времени больше. Представительные графики для всех без исключения наблюдательных скважин имеют примерно одинаковый наклон, что говорит о достаточной однородности водоносного горизонта в плане. Величина водоотдачи определяется из тех же графиков по тем же уравнениям Тейса/Купера-Джекоба. Теоретически эта величина должна быть постоянной, ибо она константа в уравнении. Однако полученный результат показывает ее закономерное изменение в зависимости от расстояния. Рис.1, построенный по нашим расчетам, показывает величину временного сдвига кривых прослеживания в зависимости от расстояния. Рис.2 показывает, как обе указанных причины влияют на расчетную величину водоотдачи. Главный вывод из этого тот, что реальный механизм водоотдачи более сложный, чем он выражен теоретически. Для нас же имеет существенное значение также то, что инерционный сдвиг от эффекта двойной пористости практически не заметен на откачной скважине. Это находится в полном соответствии с теорией (см. Приложение 1).
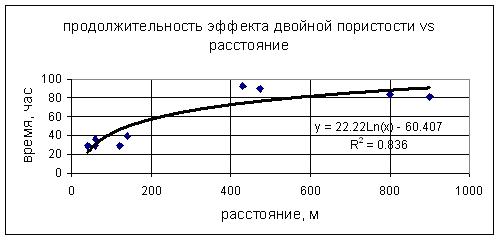
Рис.1. Продолжительность эффекта двойной пористости в зависимости от расстояния от откачной скважины
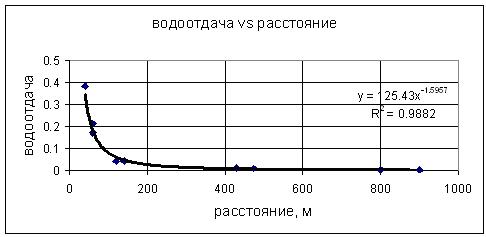
Рис.2. Водоотдача по методу Купер-Джекоб в зависимости от расстояния от откачной скважины.
Из физики явления легко предположить, что в комплексной величине водоотдачи на периферии депрессии доминирует упругая составляющая, а в центре – гравитационная. По величине они обычно разнятся примерно на два-три порядка. Уравнение Тейса/Купера-Джекоба в принципе справедливо для обоих этих режимов фильтрации, но порознь. Определить их долю на периферии депрессии не позволяет точность измерения малых величин понижения уровня там. К этому надо еще учесть, что геологическая среда неоднородна по природе своей, плюс возможное влияние внешних факторов. Это вносит дополнительную неопределенность. Вблизи откачной скважины гидравлические помехи создают модель притока, не соответствующую теоретической модели по определению. И в том и другом случае эффект двойной пористости, как правило, имеет место и тоже влияет, как показано выше. Так что теория есть, а применить проблематично. Конечно, исследовательская мысль работает, благо технические средства математического анализа позволяют все. Но вот стоит обратить внимание на программы всех научных конференций по всему миру за последнее десятилетие, чтобы заметить, что ни одна из них не проходит без научной секции, посвященной проблеме достоверности гидрогеологических оценок и прогнозов. Не устарела тревога, высказанная В.А.Мироненко и В.М.Шестаковым более тридцати лет тому назад. Более того, практика как будто разуверилась в возможности преодолеть разрыв, и пошла по пути наиболее всего ей свойственному. А именно, перестала понапрасну тратить деньги. Сейчас опытные кустовые откачки становятся скорее исключением, чем правилом. Особенно когда речь идет о глубоко залегающих горизонтах. Круг замкнулся. Нужны новые идеи.
Так совпало, что примерно в то самое время, когда была издана цитированная книга, автор озадачился проблемой привести теорию к опыту де-факто, а не наоборот, как это имеет место, т.е. опыт приспосабливают к требованию теории. Для этого надо было заново пересмотреть природу объекта. И найти «мост» для связи его с теорией. Объект, это опытная (откачная) скважина в среде со всеми своими атрибутами. При этом рассмотрении желательно обойтись без априорных натяжек или с их минимумом. Так вот задача состоит в том, чтобы данные стандартной опытной откачки из реальной скважины в пласте стали адекватными требованиям базовой теории. Этих данных должно быть достаточно, чтобы то, что невозможно реально осуществить в физическом пространстве, стало возможным представить в виртуальном пространстве. Тогда не надо будет никаких наблюдательных скважин, ни вблизи опытной скважины, ни на периферии депрессии. И еще условие. Не применять никаких дополнительных измерений и приборов. Это уже для учета инертности пользователей, традиций и экономии. А также сделать снова актуальным архив данных испытаний, произведенных в прошлом, для интерпретации с новыми возможностями.
В каждой области знания есть задачи, которые аксиоматично считаются неразрешимыми в принципе. На них как бы накладывается табу. Это одна из них. И меня угораздило на нее запасть. Не сразу. Сначала были исследования объекта вообще, понимания его сущности и функционирования. Теория и экспериментирование. Никакой связи с этой задачей, она еще не родилась. Постепенно это засасывает. Когда эти знания достигли критического объема, произошел «взрыв». В виде конкретно поставленной задачи. Этот «взрыв» произошел со мной уже в Израиле. Если бы я был в научном учреждении, меня бы, наверно, остудили. Или может быть, даже подвергли остракизму. А так я сам себе чудак. Я был не первым и не единственным, кто исследовал этот объект. Каждый до меня, его исследовал со своим взглядом на него и применительно к своей прикладной цели. Обычно исследователь подстраивает математическую модель объекта под цель, чтобы конечное решение было достижимым, удобоваримым и полезным. Так везде в прикладных науках. Так поступил и я, но, в отличие от предшественников, априори ничего не упрощал в том, что образует фундамент. Цель того требовала. И главное. Я ввел в систему уравнений компонент, который никто не рассматривал в данном контексте. Это движение потока по скважине, к которому по пути его движения присоединяются боковые притоки через фильтр. Это явление можно описать уравнением движения переменной массы с присоединением частиц по пути движения. Именно это происходит с притоком, когда он входит в скважину через фильтр и движется вдоль него к насосу, расположенному выше. Опыт применения этого уравнения к скважине уже бывал раньше. Например, для предотвращения пескования скважин путем использования фильтра с переменной перфорацией (G.Petersen, и др.,1953; Д.Ф.Шульгин,1956; Э.А.Грикевич,1969). Все эти работы, кроме факта, что они были, ничего не прибавили к данной теме.
На Рис.3 показана принятая гидравлическая модель депрессионной воронки внутри и вокруг откачной скважины. Для желающих понять смысл компонент системы, в конце статьи дается их описание в Приложении 2.
Так вот, уравнение движения переменной массы для данного объекта и задачи преобразуется в уравнение Бернулли, которое определяет баланс сил в системе. Но уравнение Бернулли справедливо для внутренних точек потока, а задача сформулирована так, чтобы выйти за его пределы, т.е. в заскважинную область. Теория поля здесь не помощник. Как это, находясь внутри источника, определить параметры среды, в которой он находится? Абсурд. Так что далее проторенной дороги нет. Начинаются новации. И первая среди них, это введенная мной новая переменная, названная «фильтрационной вязкостью». Я до сих пор сомневаюсь, удачное ли это название, но как-то стал привыкать, надеюсь, и другие привыкнут. Ее назначение - уравнять силы, приложенные к потоку внутри скважины и за ее пределами. Это сразу упрощает требования модели Тейса в определенной их части. В частности, делает систему скважина-пласт интегрально однородной гидравлически. Ввести что-либо легко, но теперь надо ее описать и найти инструмент для определения из тех же данных опыта. Из этого лабиринта уже трудно выйти на половине пути, даже если осознаешь, что заблудился. Результат почти каждого нововведения оказывался не таким как предполагался и нуждался в осознании, почему он такой. Каждая уже зафиксированная находка выдвигает потребность в поиске новой как ее продолжение. За почти двадцать лет я не смог решиться опубликовать ни одной статьи. Не было такого фрагмента, который можно было бы предъявить как нечто самостоятельное, завершенное и доказанное. И некому. Никто в мире не шел по этому пути. «Мне хорошо, я сирота».
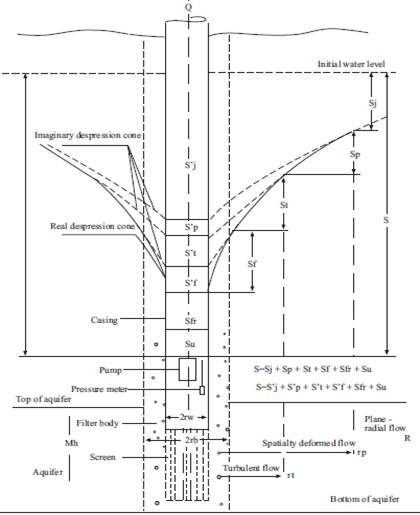
Рис.3. Общая гидравлическая модель скважины в пласте.
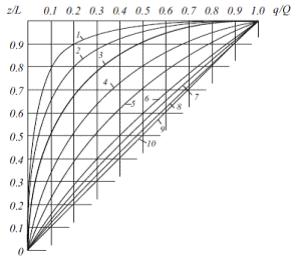 Рис.4. Теоретические кривые потока вдоль фильтра скважины. Кривые расположены в порядке убывания отношения
Рис.4. Теоретические кривые потока вдоль фильтра скважины. Кривые расположены в порядке убывания отношения  . Здесь φ иψ - комплексные безразмерные гидравлические сопротивления системы скважина-пласт для области линейного и области нелинейного режимов фильтрации соответственно.
. Здесь φ иψ - комплексные безразмерные гидравлические сопротивления системы скважина-пласт для области линейного и области нелинейного режимов фильтрации соответственно.
Так что дает введение уравнения движения переменной массы? Прежде всего, описание и понимание формы притока. Эта форма говорит о пространственной деформации поля притока из-за того, что коллектор, собирающий приток, имеет ограниченный диаметр. А его математическая форма объясняет, какими характеристиками эта деформация определяется. Т.е. величины этих характеристик определяют гидравлическую структуру этого поля. Чтобы не загружать читателя математическими выкладками (и так уже получилось длинно), покажем только несколько графических фрагментов. Так выглядит приток в реальную скважину в зависимости от соотношения величин гидравлического сопротивления областей линейного и нелинейного движения. Это показано на Рис.4.
На Рис.5. показан пример (в лабораторной модели) сравнения фактического и расчетного способов определения фрагментов депрессии: области линейного и нелинейного потока.
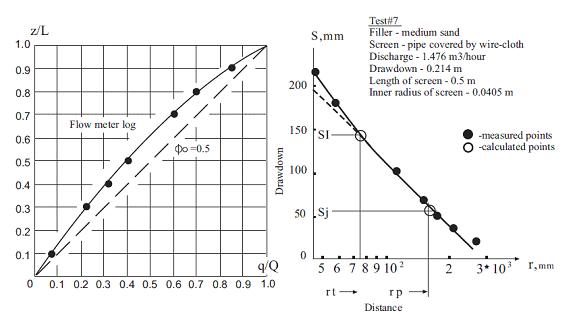
Рис.5. Пример лабораторных исследований для проверки методики.
rt - граница нелинейного режима; rp - граница упругого режима.
Ниже показана база экспериментальных данных для обоснования метода определения коэффициента фильтрационной вязкости. Она включает измерения в модели и полевые измерения. Фильтрационная вязкость имеет функциональное выражение, но для ее определения необходимо было бы ввести дополнительное измерение – глубинную расходометрию. Это не соответствует условию задачи. Но экспериментальные исследования для создания этой базы глубинную расходометрию включали обязательно. В примере на Рис.5 показано это. Их назначение в итоге создать «эталонную» зависимость для практических определений этой характеристики.
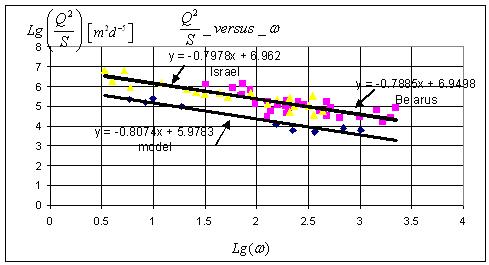
Рис.6. Конечный этап анализа экспериментальных данных для оценки коэффициента фильтрационной вязкости .
Модель принята в качестве эталона (печки). А для учета всех возможных случаев предназначен массив полевых экспериментов. Но не сам по себе. А как вспомогательное множество для разработки механизма перехода от модели к реальной единичной скважине. Такой переход от модели к реальной скважине через стандартные данные опыта был в итоге найден. Справедливость этого подхода показана на Рис.6, где он продемонстрирован на примере выборки скважин из израильских архивных данных.
Так выглядит полученная формула для универсального использования:
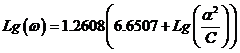 (1)
(1)
В результате имеем следующие расчетные формулы сопротивлений:
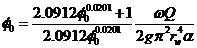 (2)
(2)
ψ0 = 2.0912φ01.0201 (3)
где 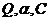 – параметры опыта;
– параметры опыта;
φ0 , ψ0 - коэффициент комплексного безразмерного гидравлического сопротивления для частного случая существования только линейного или только нелинейного режима потока во всей области соответственно.
Фрагменты депрессии определяются из следующих формул.
Внутри скважины:
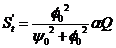 (4)
(4)
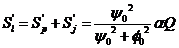 (5)
(5)
Вне скважины:
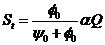 (6)
(6)
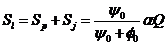 (7)
(7)
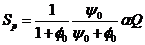 (8)
(8)
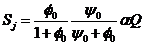 (9)
(9)
И расстояния: 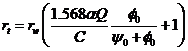 (10)
(10)
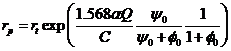 (11)
(11)
Итак, цель достигнута. Корреляция между всеми компонентами этой системы имеет определенный и устойчивый вид, что подтверждает начальную гипотезу о существовании механизма саморегулирования системы. В результате приходим к схеме опыта с виртуальными «пьезометрами» для применения классических решений подземной гидродинамики. Путь был длинным и сложным, а результат оказался простым и понятным. И ключ от этого ларчика принесло именно введение уравнения движения переменной массы с добавкой в виде коэффициента фильтрационной вязкости. Решение, о котором речь, можно назвать «подложкой» под фундаментальное решение Тейса/Купера-Джекоба для обеспечения его справедливости, где бы то ни было. Оно не имеет ограничений как методология для любой геологической среды. Данные опыта представляют собой временные функции дебита и динамики уровня в самой откачной скважине в процессе откачки, и после ее прекращения. Этих данных теперь достаточно, чтобы применить классические решения подземной гидродинамики к каждому фрагменту депрессии, вычислить гидродинамические параметры для каждого режима фильтрации и многое другое, характеризующее водоносный горизонт в пределах созданной депрессии. И все работает теперь исправно в соответствии с теорией и без противоречий с практикой. И даже в более приемлемом для нее виде.
Состоялось несколько апробаций на международных мероприятиях: (International Exhibition WATEC, Tel-Aviv, 2007) и (International Symposium IAHR, Istanbul, 2008). Мои впечатления от реакции аудитории остались самые благоприятные. Пришло время и для более серьезных публикаций.
Ниже в Приложении 3 показана схематично структура Программного Обеспечения Pumping Well Test Software. В Приложении 4 приведен типичный пример исходных данных опыта и результата применения ПО Pumping Well Test Software.
Итак, задача решена и доказана. Частная, на первый взгляд, теоретическая и техническая задача. Но кто в теме, тот понимает, что потенциально это сэкономленные миллионы денег от теперь ненужного бурения и связанных с ним работ, от сокращения затрат труда и времени на проведение полевых опытов. Во что обходится обеспечение достоверности гидрогеологических расчетов и прогнозов, или, ущерб от недостаточного уровня достоверности, это особая статья для оценивания экономических последствий профессионалами в этой области.
Каково же состояние с использованием? Нечем хвастать. Пока только израильская Национальная Водная компания Мекорот, которая способствовала разработке, теперь использует переданную ей программу Pumping Well Test Software. Для распространения использования этой методологии и Программного Обеспечения в мире нужны инвестиции для пропаганды и поддержки. Но это пока не привлекает инвесторов. Не звучит, видимо. Или кризисное состояние мировой экономики сдерживает. Здесь надо клевать по зернышку, а не так, чтобы оптом купил – продал. Вот и настигли меня недостатки свободного творчества. Судьба результата свободного творчества в науке, – это беспризорность.
А что в нефтяной геологии, может спросить внимательный читатель. Ведь законы гидродинамики те же и теории те же. А отрасль серьезная и процветает. Все верно. Законы никто не отменял. В том числе и результат. И все же, чтобы ответ был полным, приведу факт. У нефтяников в ходу следующая формула для оценки коэффициента нефтеотдачи (аналог водоотдачи), которая в русской нефтяной литературе известна как формула В.Н.Щелкачева:
μ = Μ η (m βf + βt), ,
где
Μ и m - мощность пласта, и его пористость соответственно; η - вязкость флюида; βf, βt - сжимаемость флюида и скелета породы соответственно. Как видно, это другая технология. А все по той же причине. Здесь и керновое бурение на продуктивных глубинах, и приборы для глубинных геофизических и других измерений, и лаборатории для петрофизических, компрессионных и реологических измерений, и многое другое. Зная точность определения компонент этой функции, получим, что результат будет иметь точность в пределах порядка. Условия добычи нефти много сложнее и требуют более тщательного надзора и ухода за парком эксплуатационных скважин, в том числе приложения гидродинамических методов исследования на этой стадии. В основном используется метод восстановления давления (КВД). Для этого скважина выводится из эксплуатации, иногда на продолжительное время. Но только этого, оказывается, недостаточно. Приходится использовать еще эмпирику. Нефть потому и дороже воды, что дороже обходится. С предложенным нами вариантом анализа гидродинамических данных многое стало бы проще и однозначно. Чтобы ощутить масштаб, приведу цифры. От применения описанной разработки общая годовая экономия в мире составила бы в отрасли подземные воды 2.0 млрд. долларов. В нефтедобывающей отрасли (после надлежащей адаптации) это было бы 30.0 млрд. долларов. Но нефть, это все же другая тема.
***********
Из ранее опубликованных работ автора, которые предшествовали разработке этой методологии, можно назвать следующие, как основные:
1. Гершанович И.М., Гидрогеологические исследования в скважинах методом расходометрии, М., Недра, 1981. 295с.
2. Гершанович И.М., Дядиченко В.М., Дядиченко Е.М., Экспериментальная оценка точности определения зоны нарушения линейного режима фильтрации методом расходометрии возмущающей скважины. Сб. Физическое моделирование гидрогеологических и инженерно-геологических процессов. М., ВСЕГИНГЕО, 1986.
* * *
Приложение 1.
Эти выкладки приведены для справки, хотя, в этой статье можно было бы обойтись без них. В то же время это тот фундамент, на который я ссылаюсь, и тот «шаблон», который делаю справедливым для применения в реальных условиях одиночной скважины. Поэтому они приведены здесь для полноты изложения предмета.
Снижение уровня (напора, давления) в пласте при откачке представляется следующим дифференциальным уравнением:
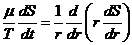 (1.1)
(1.1)
Понижение уровня на площади депрессии для откачки с дебитом и граничными условиями:
S(r,0) = 0 (нулевой начальный уровень),
S(∞,t) = 0 (внешние источники отсутствуют),
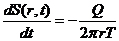 (1.2)
(1.2)
выражается по (Theis C.V., 1935. The relation between lowering of the piezometric surface and the rate and duration of discharge of a well using ground water storage, Trans. Am. Geophys. Un., Pt. 2, 519-524) уравнением:
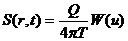 , (1.3)
, (1.3)
где
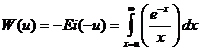 ,
,
W(u) называется функцией скважины 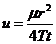 ,
,
T - водопроводимость,
μ – водоотдача, для напорного пласта упругая водоотдача (elastic storativity),
r - расстояние,
t - время.
Для , т.е. при больших временах и/или малых расстояниях, функция может быть представлена в виде линейной функции (Cooper H.H.Jr. and C.E. Jacob, 1946. A generalized graphical method for evaluating formation constants and summarizing well field history, Trans. Am. Geophys. Un., 27, 526-634):
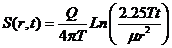 , (1.4)
, (1.4)
от аргументов: 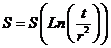 , или
, или 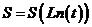 , или
, или 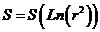 .
.
Приложение 2.
Депрессионная воронка вокруг откачной скважины является следствием откачки с заданным дебитом и комплексного влияния различных гидравлических сопротивлений в системе скважина-пласт. Концептуальная модель, принятая для решения, исходит из предпосылки, что потеря напора внутри скважины и вокруг нее представляет собой саморегулирующуюся систему с постоянными соотношениями. Это положение было проверено несколькими способами.
На рисунке показана концептуальная схема системы скважина-пласт. Что касается гидравлики, выделяется зона линейного и нелинейного потока, последовательно сменяющие друг друга от периферии к центру воронки депрессии. Поле течения считается пространственным, осе симметричным. Другие условия являются аналогичными общепринятым в классической постановке: водоносный горизонт является горизонтальным, однородным, изотропным, бесконечным в плане, имеет конечную мощность. Структура гидравлического поля состоит из следующих компонент потери напора внутри и за пределами откачной скважины. Символ (,) означает, что указанная величина принадлежит пространству внутри скважины, отсутствие этого символа относится к заскважинному пространству.
S - суммарная потеря напора внутри скважины.
S,j – потеря напора на участке R - rw . Принимается, что при Q = Const условие и решение Тейс/Купер-Джекоб является справедливым для этого участка фильтрации.
Sj – потеря напора на участке R - rp . Принимается, что при Q = Const условие и решение Тейс/Купер-Джекоб является справедливым для этого участка фильтрации.
S,p – приращение потери напора внутри скважины r = rw . Оно характеризует отклонение от модели фильтрации по Тейс/Купер-Джекоб по причине искривления поля на входе в скважину, подобно эффекту неполного вскрытия мощности.
Sp – доля потери напора на участке rp = rt . Она считается результатом отклонения от модели по Тейс/Купер-Джекоб по причине искривления поля на входе в скважину, подобно эффекту неполного вскрытия мощности. Принимается, что линейный режим фильтрации сохраняется во всей этой области.
S,t – приращение потери напора внутри скважины в результате турбулизации потока на участке rt = rw .Принимается условно, что этот интервал сложен из материнского материала пласта.
St – доля потери напора на участке rp = rw . Она считается вызванной турбулизацией потока на этом интервале фильтрации. Принимается условно, что этот интервал сложен из материнского материала пласта.
S,f – приращение потери напора внутри скважины из-за гидравлического сопротивления тела фильтра.
Sf – доля потери напора на теле фильтра мощностью rb = rw из-за его гидравлического сопротивления.
Sfr – потеря напора из-за гидравлического сопротивления трения внутренней поверхности фильтра и обсадной колонны.
Su - потеря напора по какой-либо неопределенной причине.
Mh - мощность пласта, обеспечивающая приток.
R – радиус влияния откачки.
L – длина фильтра.
rb - радиус скважины по бурению.
rw - внутренний радиус фильтра.
rp – радиус интервала, где происходит смена режима фильтрации от упругого на гравитационный.
rt - радиус турбулизации потока.
В общем случае, S,p , Sp , S,t , St , S,f, Sf и Sfr являются функциями z – глубина от подошвы фильтра. S,j и Sj – не зависят от координаты z , как это принято в модели Тейс/Купер-Джекоб.
Приложение 3.
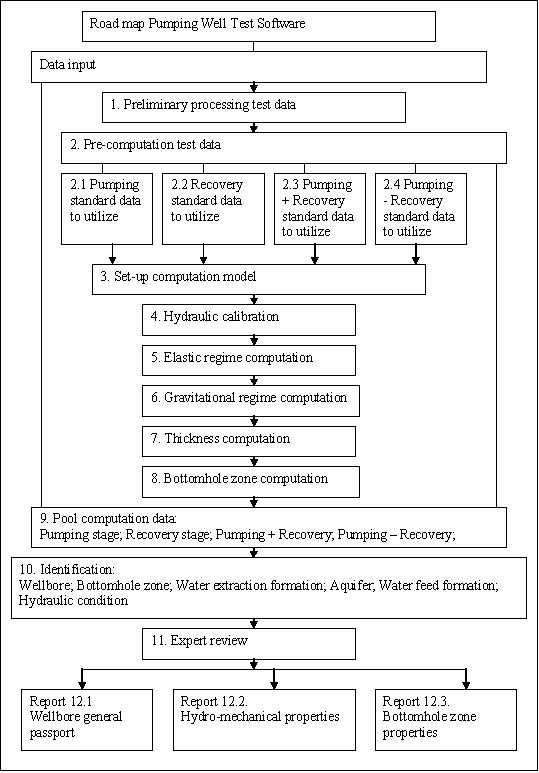
Рис.7
Приложение 4.
Pumping Well Test Software в действии.
Приведен пример из практики в Израиле. На Рис.8 приведен разрез продуктивной скважины в известковых песчаниках Плейстоцена. Скважина оборудована фильтром Джонсона с гравийной обсыпкой. Другие технические характеристики скважины приведены в рисунке. Пример приводится без каких-либо комментариев или разъяснений результата. Профессиональный читатель, при желании, сам в состоянии оценить его на основании своих знаний в гидрогеологии, петрофизике, технике строительства скважин.
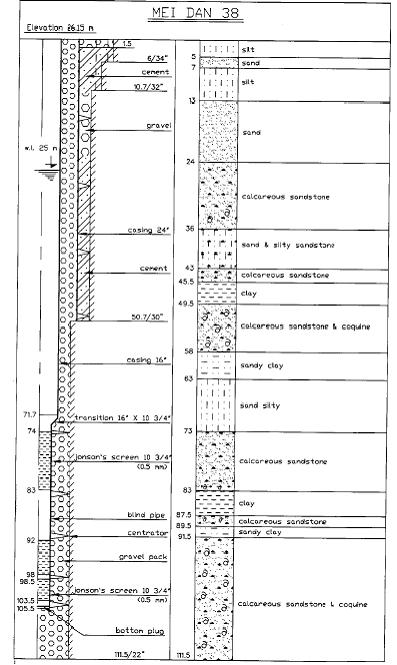
Рис.8
Титул ПО

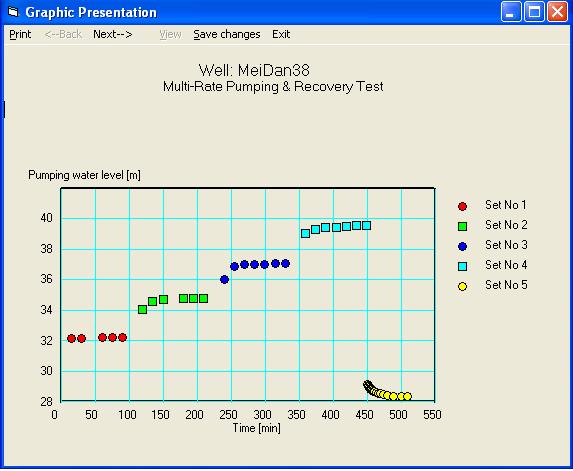
Рис.9. Исходные данные динамики уровня в скважине при откачке.
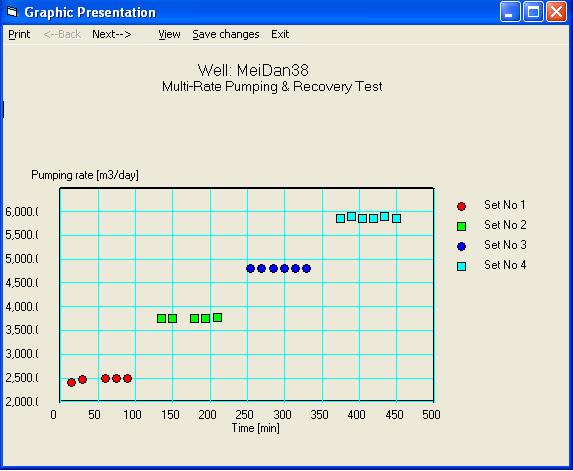
Рис.10 Исходные данные дебита скважины при откачке.
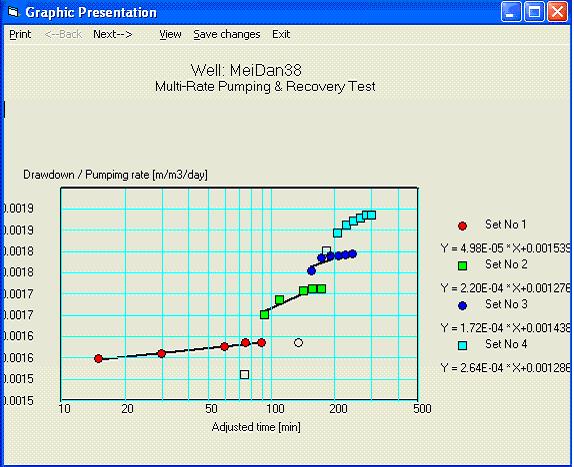
Рис.11. Интерактивная обработка экспериментальных данных. Это единственное место, где Программное Обеспечение предлагает пользователю принять участие в процессе обработки данных.
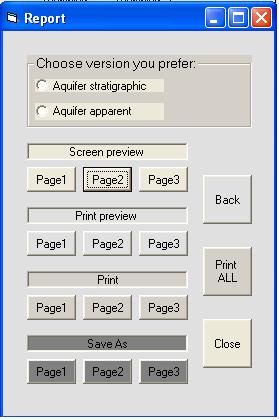
Рис.12. Выбор варианта отчета.
После выбора варианта появляется доступ к Screen preview Page 2 таблице результата для этого варианта. При желании поменять вариант, пользователь выходит командой Close, указывает другой вариант, и снова входит в Page 2 Screen preview и все повторяется, столько раз, сколько пользователь хочет. Если появилось желание пересмотреть процедуру предварительной обработки данных, показанную на Рис.11, команда Back вернет пользователя к началу интерактивного процесса программы. Последний из просмотренных вариантов запоминается по умолчанию как конечный для черно-белого печатного отчета или для сохранения в желаемой директории.
Отчет. Общие сведения о скважине и опыте.
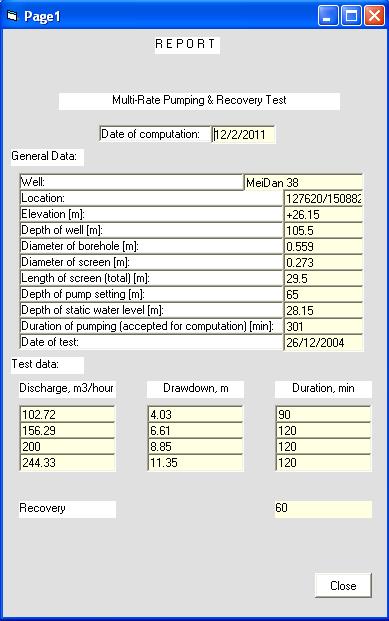
Рис.13
Отчет. Так выглядит результат оценки свойств и характеристик водоносного горизонта. Вариант, в котором мощность водоносного горизонта соответствует модели Тейс/Купер-Джекоб по Н.Н.Веригину, 1959.
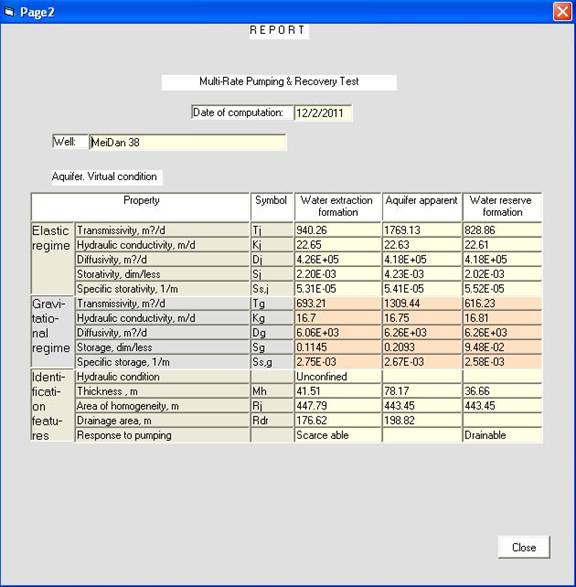
Рис.14
Отчет. Так выглядит результат оценки свойств и характеристик водоносного горизонта. Вариант, в котором мощность водоносного горизонта соответствует стратиграфическому строению разреза.
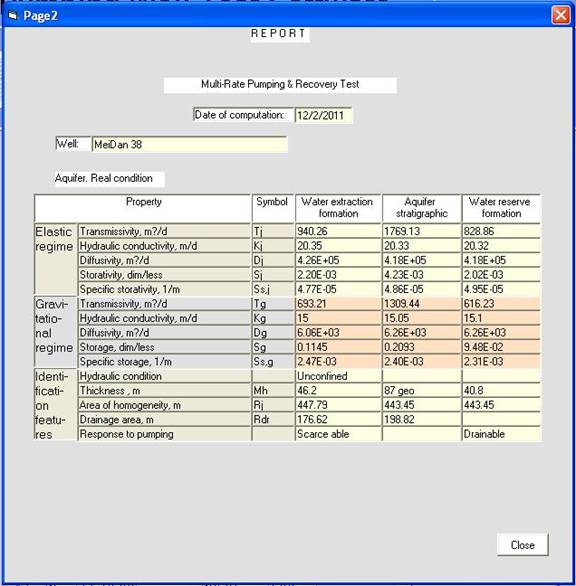
Рис.15
Отчет. Так выглядит результат оценки свойств и характеристик скважины и ее ближней зоны.
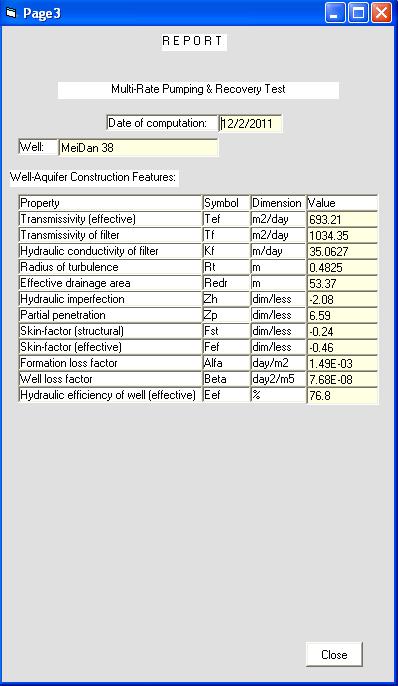
Рис.16
----------------------------------------------------------------------------------
Статья прислана автором 26 октября 2011 г.
для обсуждения на семинаре







